



Next: Geometrical calibration
Up: Calibrating ALIS
Previous: Removing the instrument signature
Contents
Index
Subsections
Intercalibration
Intercalibration is carried out in order to be able to compare
measurements from different instruments. To facilitate this, three
radioactive 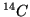 light-standards and a calibration lamp are used
(Figure 4.2).
light-standards and a calibration lamp are used
(Figure 4.2).
Figure 4.2:
Top: The three 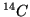 phosphor light-standards with phosphor:
Y-275, L-1614 and 920-B. Lower right: A calibration source with a
tungsten lamp. (To the lower left are some parts from a calibration
source based on a fluorescent light)
phosphor light-standards with phosphor:
Y-275, L-1614 and 920-B. Lower right: A calibration source with a
tungsten lamp. (To the lower left are some parts from a calibration
source based on a fluorescent light)
|
|
These light-standards are intercalibrated against other light
standards during European calibration workshops held at regular
intervals
[for example Lauche and Widell, 2000a; Lauche and Widell, 2000b; Widell and Henricson, 2001]. As
several of the light-standards used at these intercalibration sessions
are traceable to National Bureau of Standards (NBS) sources,
it is thus also possible to perform absolute calibration
[Torr and Espy, 1981]. Results from some of the most recent
calibration workshops are summarised in Table 4.3.
Table 4.3:
Results from a selection of recent intercalibration workshops:
The column emission rates are given in
[R/Å] (Rayleighs/Ångströ).
(Some sources have been omitted in order to fit the table on one page.)
[after Lauche and Widell, 2000a; Lauche and Widell, 2000b; Widell and Henricson, 2001, and earlier calibration workshop reports]
|
Sources |
Column emission rate [R/Å] at Filter [Å] |
|
calibration |
year |
3914 |
4280 |
4866 |
5573 |
5882 |
6299 |
6562 |
|
Esrange, tungsten lamp |
|
|
|
|
|
|
|
|
Stockholm |
2000 |
1.3 |
4.1 |
30 |
212 |
310 |
532 |
553 |
|
Oulu |
2001 |
0.53 |
1.5 |
11.6 |
82 |
122 |
233 |
171 |
|
IRF, UJO 920B |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
5.1 |
126.0 |
61.5 |
18.6 |
10.5 |
6.7 |
8.1 |
|
Lindau |
1999 |
4.4 |
102 |
60 |
22 |
12 |
7.6 |
2.4 |
|
Stockholm |
2000 |
4.6 |
109 |
64 |
23 |
12.7 |
10 |
8.5 |
|
Oulu |
2001 |
5.2 |
105 |
65 |
22 |
13 |
9.2 |
1.2 |
|
IRF, UJO L1614 |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
0.07 |
0.73 |
32.5 |
27.7 |
8.7 |
2.5 |
4.3 |
|
Lindau |
1999 |
0.6 |
1 |
37 |
33 |
9.3 |
1 |
2 |
|
Stockholm |
2000 |
0.07 |
1.0 |
40 |
35 |
9.6 |
0.36 |
0.57 |
|
Oulu |
2001 |
0.1 |
1.1 |
38 |
27 |
7 |
1.2 |
10.2 |
|
IRF, UJO Y275 |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
0.03 |
0.3 |
3.8 |
251.0 |
378.0 |
217.0 |
113.0 |
|
Lindau |
1999 |
0.01 |
0.2 |
3.8 |
263 |
383 |
282 |
165 |
|
Stockholm |
2000 |
0.01 |
0.22 |
3.9 |
276 |
405 |
282 |
181 |
|
Oulu |
2001 |
0.002 |
0.18 |
3.6 |
258 |
482 |
274 |
155 |
|
Mike Taylor, source |
|
|
|
|
|
|
|
|
Stockholm |
2000 |
0.03 |
0.98 |
6.8 |
10 |
1.8 |
0.3 |
2.5 |
|
<#7545#>Sodankylä, |
|
|
|
|
|
|
|
|
blue lamp |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
2.0 |
6.0 |
10.1 |
9.9 |
15.3 |
4.0 |
0.66 |
|
Lindau |
1999 |
2.3 |
7.2 |
12 |
9.3 |
10 |
7.5 |
7.2 |
|
Stockholm |
2000 |
2.5 |
7.3 |
12.5 |
9.3 |
9.5 |
6.3 |
2.8 |
|
Oulu |
2001 |
2.6 |
7.6 |
12 |
8.9 |
13 |
10 |
12 |
|
<#7551#>Sodankylä, |
|
|
|
|
|
|
|
|
tungsten lamp |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
0.12 |
0.71 |
5.4 |
31.8 |
62.8 |
125.8 |
137 |
|
Lindau |
1999 |
0.1 |
0.75 |
5.6 |
33.5 |
65 |
137 |
192 |
|
Stockholm |
2000 |
0.10 |
0.65 |
5.2 |
31 |
61 |
139 |
285 |
|
Oulu |
2001 |
0.01 |
0.6 |
5 |
30 |
75 |
133 |
248 |
|
IRF, tungsten lamp |
|
|
|
|
|
|
|
|
Stockholm |
2000 |
0.19 |
1.1 |
8.5 |
50 |
98 |
223 |
454 |
|
Oulu |
2001 |
0.17 |
1.2 |
8 |
48 |
115 |
228 |
428 |
|
MPI-2 lamp |
|
|
|
|
|
|
|
|
Lysebu |
1985 |
0.02 |
0.16 |
2.43 |
193.7 |
290.7 |
191.8 |
98.2 |
|
Lindau |
1999 |
0.03 |
0.12 |
2.2 |
172 |
258 |
213 |
235 |
|
Stockholm |
2000 |
0.01 |
0.13 |
2.3 |
175 |
266 |
153 |
105 |
|
Oulu |
2001 |
0.01 |
0.01 |
2.3 |
169 |
251 |
193 |
105 |
|
S.Chernouss, Glow lamp |
|
|
|
|
|
|
|
|
Oulu |
2001 |
13 |
143 |
66 |
84 |
374 |
392 |
59 |
|
S.Chernouss, Tungsten |
|
|
|
|
|
|
|
|
Oulu |
2001 |
0.01 |
1.6 |
5.5 |
36 |
293 |
947 |
679 |
|
For the 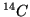 -sources in use for calibrating ALIS (phosphors: 920B,
L1614 and Y275) the column emission rate is plotted against wavelength
in Figure 4.3.
-sources in use for calibrating ALIS (phosphors: 920B,
L1614 and Y275) the column emission rate is plotted against wavelength
in Figure 4.3.
Figure 4.3:
Column emission rates [R/Å] as a function of wavelength [Å] for
the three radioactive 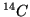 light-standards with phosphor: 920-B
(blue line), L-1614 (green line) and Y-275 (red line). These plots
also include intercalibration results from the Aberdeen 1980
workshop [Torr and Espy, 1981]. These values are not shown in
Table 4.3. Legend: Intercalibration sessions of 1981 'x'
1985 '+', 1999 '*', 2000 'o' , and 2001 '
light-standards with phosphor: 920-B
(blue line), L-1614 (green line) and Y-275 (red line). These plots
also include intercalibration results from the Aberdeen 1980
workshop [Torr and Espy, 1981]. These values are not shown in
Table 4.3. Legend: Intercalibration sessions of 1981 'x'
1985 '+', 1999 '*', 2000 'o' , and 2001 ' '. The lines
connect the results from the latest calibration workshop, held in
Oulu 2001. (The last points on these lines for the L1614 and 920B
calibrators are probably measurement errors)
'. The lines
connect the results from the latest calibration workshop, held in
Oulu 2001. (The last points on these lines for the L1614 and 920B
calibrators are probably measurement errors)
|
|
Table 4.4 presents the ratios of column emission rates
Table 4.4:
Ratios of results from the latest calibration workshop
[Oulu, 2002, see Widell and Henricson, 2001] to earlier calibration sessions.
Bold face indicates results for wavelengths where the calibrators are
most commonly used. See also Table 4.3 and Figure 4.3
|
Source |
Year |
column emission ratios (2001/year) at Filter [Å] |
|
|
|
3914 |
4280 |
4866 |
5573 |
5882 |
6299 |
6562 |
|
y275 |
1985 |
0.07 |
0.60 |
0.95 |
1.03 |
1.28 |
1.26 |
1.37 |
|
y275 |
1999 |
0.20 |
0.90 |
0.95 |
0.98 |
1.26 |
0.97 |
0.94 |
|
y275 |
2000 |
0.20 |
0.82 |
0.92 |
0.93 |
1.19 |
0.97 |
0.86 |
|
l1614 |
1985 |
1.43 |
1.51 |
1.17 |
0.97 |
0.80 |
0.48 |
2.37 |
|
l1614 |
1999 |
0.17 |
1.10 |
1.03 |
0.82 |
0.75 |
1.20 |
5.10 |
|
l1614 |
2000 |
1.43 |
1.10 |
0.95 |
0.77 |
0.73 |
3.33 |
17.89 |
|
920b |
1985 |
1.02 |
0.83 |
1.06 |
1.18 |
1.24 |
1.37 |
0.15 |
|
920b |
1999 |
1.18 |
1.03 |
1.08 |
1.00 |
1.08 |
1.21 |
0.50 |
|
920b |
2000 |
1.13 |
0.96 |
1.02 |
0.96 |
1.02 |
0.92 |
0.14 |
|
from the latest calibration workshop (Oulu, 2001) to earlier
calibration sessions. Despite the 5730 years half-life of 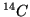 ,
deviations of 10-20% are present, even within a couple of years as
also noted by Kaila and Holma [2000]. This is probably related to
either errors in the intercalibration procedure, or to the
light-emitting phosphor of the sources.
,
deviations of 10-20% are present, even within a couple of years as
also noted by Kaila and Holma [2000]. This is probably related to
either errors in the intercalibration procedure, or to the
light-emitting phosphor of the sources.
The original use of these light-standards has been to calibrate
photometers. This has been done by placing the light-standard on top
of the front-lens of the photometer, covering the entire
field-of-view. The same procedure was followed when calibrating the
ALIS imagers. As the light-emitting surface of the calibrator does not
cover the entire field-of-view of the imager, this method has been
questioned [Gustavsson, 1997]. Therefore, during the latest
calibration workshop, the light sources were placed at a larger
distance (within focus) of the imager. However due to various
technical problems, the results were inconclusive. Therefore this
question remains open.
Absolute calibration
The digital-output,
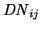 , and number of generated
photo-electrons per pixel
, and number of generated
photo-electrons per pixel
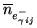 is related by:
is related by:
![$\displaystyle \mathit{DN}_{ij}=G_{S}\ \overline{n}_{e^{-}_{\gamma{}ij}} \left[\mathrm{counts}\right]$](img416.png) |
(4.7) |
where 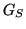 is the imager system gain,
[Preston, 1995; Preston, 1993]:
is the imager system gain,
[Preston, 1995; Preston, 1993]:
![$\displaystyle G_{S}=\frac{G_{CCD}\ G_{P}\ t_{DCS}}{B_{ADC}\ \tau_{DCS}} \left[\frac{\mathrm{counts}}{e^{-}_{\gamma}}\right]$](img419.png) |
(4.8) |
Here, 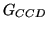 is the CCD output
sensitivity,
is the CCD output
sensitivity,
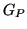 is the programmable gain setting (5 or 10),
is the programmable gain setting (5 or 10),
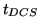 is the DCS integration time,
is the DCS integration time,
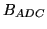 is the ADC bit weight
(
is the ADC bit weight
(
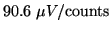 ), and
), and
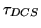 is the DCS integrator time constant.
These parameters are configured during CCU start-up
(Section 3.3.3).
is the DCS integrator time constant.
These parameters are configured during CCU start-up
(Section 3.3.3).
Combining Equation 4.6 with Equations 3.20 and 3.22 yields for
uniformly illuminated central pixels of the
CCD,
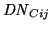 :
:
![$\displaystyle \frac{I_{cal}}{\mathit{DN}_{Cij}}= \frac{1}{t_{\mathit{int}}}\, \...
...0^{10}\, G_{s}\, {Q_{E}}\, T\, A_{pix}}\ \left[\frac{R}{\mathrm{counts}}\right]$](img430.png) |
(4.9) |
The ``known'' column emission rate, 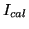 , which
is obtained from a light-standard by integrating over the
filter passband,
, which
is obtained from a light-standard by integrating over the
filter passband,
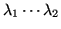 is
given by:
is
given by:
![$\displaystyle I_{cal}=\int_{\lambda_{1}}^{\lambda_{2}} I_{ls}(\lambda)\, d\lambda \approx I_{ls}(\lambda_{2}-\lambda_{1})=I_{ls}\, \Delta\lambda \left[R\right]$](img434.png) |
(4.10) |
Here, the column emission rate of the light
standard,
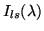 , is a function of wavelength
, is a function of wavelength
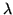 , that must be integrated over the filter
passband,
, that must be integrated over the filter
passband,
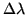 . However during the
intercalibration workshops,
. However during the
intercalibration workshops,
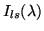 is measured only for one
wavelength in the filter passband, hence the approximation in
Equation 4.10 (see Table 4.3 and Figure 4.3).
is measured only for one
wavelength in the filter passband, hence the approximation in
Equation 4.10 (see Table 4.3 and Figure 4.3).
Now, consider the right-hand part of Equation 4.9. The
quantum-efficiency, transmittance and system gain is a function of
wavelength and pixel-coordinates among other things, such as for example
filter-temperature (i.e.
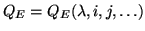 ,
,
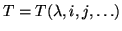 and
and
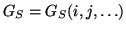 ). Due to the
difficulties of determining these functions as well as the
approximations and uncertainties related to the
). Due to the
difficulties of determining these functions as well as the
approximations and uncertainties related to the 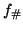 Equation 4.9 is
rewritten as follows:
Equation 4.9 is
rewritten as follows:
![$\displaystyle \frac{I_{cal}}{\mathit{DN}_{Cij}}= \frac{1}{t_{\mathit{int}}}\, C_{abs\lambda{c}}\, \mathit{F}_{ij\lambda} \ \left[\frac{R}{\mathrm{counts}}\right]$](img440.png) |
(4.11) |
Here
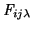 (Equation 4.4) corrects for both the dependence
on pixel-coordinates as well as on wavelength for a particular filter.
(The index
(Equation 4.4) corrects for both the dependence
on pixel-coordinates as well as on wavelength for a particular filter.
(The index
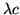 in the absolute calibration
constant,
in the absolute calibration
constant,
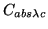 , indicates that the
constant is unique for each filter of each imager
, indicates that the
constant is unique for each filter of each imager 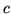 ). Hence,
the importance of a proper flat-field calibration cannot be
underestimated (Section 4.1.3). Unfortunately, a proper
flat-field calibration is not yet available for ALIS, and some
approximations are required:
). Hence,
the importance of a proper flat-field calibration cannot be
underestimated (Section 4.1.3). Unfortunately, a proper
flat-field calibration is not yet available for ALIS, and some
approximations are required:
![$\displaystyle \frac{I_{cal}}{\mathit{DN}_{Cij}}\approx \frac{1}{t_{\mathit{int}...
...{abs\lambda{c}} \mathit{F}_{Mij\lambda}\ \left[\frac{R}{\mathrm{counts}}\right]$](img444.png) |
(4.12) |
In this case the modelled flat-field correction
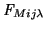 of Equation 4.6 is used together with a
normalised filter transmittance
function,
of Equation 4.6 is used together with a
normalised filter transmittance
function,
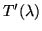 , by integrating over the
vendor-provided filter transmittance curve and normalising (i.e. set
, by integrating over the
vendor-provided filter transmittance curve and normalising (i.e. set
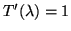 ) at peak filter transmittance (Figure 4.4).
) at peak filter transmittance (Figure 4.4).
Figure 4.4:
Example filter transmittance curve
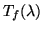 as
measured by the filter manufacturer for a 40 Å wide 5590 Å filter
(Lot. No. 3697). The measured peak transmittance of the filter is
0.6 and the centre wavelength at normal incidence
(
as
measured by the filter manufacturer for a 40 Å wide 5590 Å filter
(Lot. No. 3697). The measured peak transmittance of the filter is
0.6 and the centre wavelength at normal incidence
(
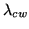 ) and filter bandwidth is measured to
5587.2 Å and 38.4 Å respectively. This filter is intended for
the
) and filter bandwidth is measured to
5587.2 Å and 38.4 Å respectively. This filter is intended for
the 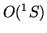 5577 Å auroral emission line. The deviation from normal
incidence shifts the centre wavelength, which explains why a
centre wavelength of 5590 Å was selected, (see Equation 3.45 in
Section 3.5). As can be seen, this filter has a rather uniform
transmittance in the passband.
5577 Å auroral emission line. The deviation from normal
incidence shifts the centre wavelength, which explains why a
centre wavelength of 5590 Å was selected, (see Equation 3.45 in
Section 3.5). As can be seen, this filter has a rather uniform
transmittance in the passband.
|
|
However for most filters it is acceptable to take
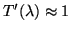 over the entire filter-passband.
Equations 4.5 and 4.11 yield the following equation (substituting
Equation 4.10) to be used when a proper flat-field calibration is
available:
over the entire filter-passband.
Equations 4.5 and 4.11 yield the following equation (substituting
Equation 4.10) to be used when a proper flat-field calibration is
available:
![$\displaystyle C_{abs\lambda{c}}=\frac{1}{\overline{\mathit{DN}}'_{C}} \int_{\la...
...\lambda_{2}} I_{ls}(\lambda)\, d\lambda\ \left[\frac{R}{\mathrm{counts}}\right]$](img450.png) |
(4.13) |
where
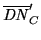 is obtained by averaging together a
number of uniformly illuminated pixels in the central part of the
image.
is obtained by averaging together a
number of uniformly illuminated pixels in the central part of the
image.
The present more approximative calibration is described by
Equations 4.6 and 4.12:
![$\displaystyle C_{abs\lambda{c}}\approx \frac{1}{\overline{\mathit{DN}}'_{C}} \i...
...ta\lambda}{\overline{\mathit{DN}}'_{C}}\ \left[\frac{R}{\mathrm{counts}}\right]$](img452.png) |
(4.14) |
Hence, an absolute-calibration must be carried out for each filter
of each imager.
The results from the two most recent absolute calibrations of the ALIS
imagers are found in Table 4.5.
Table 4.5:
Calibration results from ALIS obtained in 1996 and 1997. The large difference
for ccdcam1 occurs because it was equipped with filter-wheel and new
optics between these calibrations. Some filters
(see Tables 3.4 and 3.5),
as well as ccdcam6
were not yet available during these calibrations. Both calibrations used the
Lysebu, 1985 intercalibration. The last column gives values of the
calibration of 21 May 1997, adjusted by the 2001 intercalibration result (Table 4.3).
Finally it should be noted that no suitable light-standard for calibration
of the 8455 Å filters is available.
|
|
|
|
|
96-07-10 |
97-05-21 |
2001 adj. |
|
ccd |
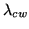 |
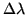 |
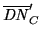 |
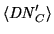 |
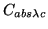 |
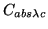 |
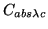 |
|
cam |
[Å] |
[Å] |
![$ [\mathrm{counts}]$](img193.png) |
![$ [\mathrm{counts}]$](img193.png) |
![$ [\mathrm{R}/\mathrm{counts}]$](img455.png) |
![$ [\mathrm{R}/\mathrm{counts}]$](img455.png) |
![$ [\mathrm{R}/\mathrm{counts}]$](img455.png) |
|
1 |
5590 |
40 |
217.5 |
2.6 |
32.4 |
46.2 |
47.4 |
|
1 |
6310 |
40 |
173.4 |
2.6 |
|
50.1 |
63.2 |
|
1 |
6230 |
40 |
254.2 |
2.9 |
|
34.1 |
43.1 |
|
1 |
4285 |
50 |
116.8 |
3.4 |
|
53.9 |
44.9 |
|
2 |
5590 |
40 |
300.6 |
3.6 |
28.2 |
33.4 |
34.3 |
|
2 |
6310 |
40 |
339.3 |
3.5 |
25.6 |
25.6 |
32.3 |
|
3 |
5590 |
40 |
484.2 |
4.1 |
21.9 |
20.7 |
21.3 |
|
3 |
6310 |
40 |
427.3 |
2.8 |
22.2 |
20.3 |
25.6 |
|
4 |
5590 |
40 |
468.0 |
5.3 |
23.7 |
21.5 |
22.1 |
|
4 |
6310 |
40 |
402.2 |
4.1 |
23.7 |
21.6 |
27.3 |
|
5 |
5590 |
40 |
333.8 |
4.0 |
|
30.1 |
30.9 |
|
5 |
6310 |
40 |
390.5 |
4.2 |
|
22.2 |
28.1 |
|
As can be seen, the last absolute calibration of the ALIS imagers was
carried out in 1997. At that time ccdcam6 was not yet
delivered; neither were all filters available. Also no suitable
light-standard is available for the near-infrared 8446 Å emission
line. An attempt was made to perform a re-calibration of all imagers
and filters in 2001. However this effort failed due to technical
problems and limited time. Hence a new calibration must be
performed as soon as possible.
A comparison of auroral measurements from ccdcam6 and a
Russian photometer (calibrated in Russia) both co-located in Kiruna
indicates a disagreement in absolute intensities of
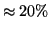 between the two instruments [Sergienko, 2003]. This comparison
as well as extrapolated values have been in use for the filter/imager
combinations not appearing in Table 4.5 (i.e.
ccdcam6. See also Tables 3.4 and
3.5).
between the two instruments [Sergienko, 2003]. This comparison
as well as extrapolated values have been in use for the filter/imager
combinations not appearing in Table 4.5 (i.e.
ccdcam6. See also Tables 3.4 and
3.5).
There is furthermore an interesting possibility of performing absolute
calibration by using known spectra of stars, which has been done for
the 8446 Å emission-line [Gustavsson, 2003]. This method would
simplify the calibration procedures considerably. However this is a
new method and these results have yet to be intercalibrated with the
present calibration method. Regardless of whether the new method will be a
verification procedure, or replace the present calibration procedure,
it will no doubt represent a major improvement of the absolute
calibration for ALIS.
Due to the inherent difficulties of absolute intensity calibration, an
error of the order of 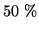 is often regarded as acceptable. The
largest errors appear to be related to the intercalibration of the
light-standards (about 10-20 %, refer to Table 4.4).
Furthermore, the calibration results appear to be fairly stable over one
year (Table 4.5). On the other hand there are still many
uncertain factors in the calibration procedure, most notably the
absence of a uniform source needed for the flat-field calibration
(Section 4.1.3). Therefore, to be on the safe side, it might be
stated that the absolute calibration error lies in the range of
25-50 %. The intercalibration error of the ALIS imagers is probably
much lower, at least for pixels in the central region of the image.
For an imaging instrument, these errors are probably to be considered
as acceptable. However improvements are still required.
is often regarded as acceptable. The
largest errors appear to be related to the intercalibration of the
light-standards (about 10-20 %, refer to Table 4.4).
Furthermore, the calibration results appear to be fairly stable over one
year (Table 4.5). On the other hand there are still many
uncertain factors in the calibration procedure, most notably the
absence of a uniform source needed for the flat-field calibration
(Section 4.1.3). Therefore, to be on the safe side, it might be
stated that the absolute calibration error lies in the range of
25-50 %. The intercalibration error of the ALIS imagers is probably
much lower, at least for pixels in the central region of the image.
For an imaging instrument, these errors are probably to be considered
as acceptable. However improvements are still required.
Finally, the absolute calibration is applied to the object-images
(
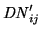 , see Equations 4.5 and 4.6):
, see Equations 4.5 and 4.6):
![$\displaystyle I_{ij}=C_{abs\lambda{c}}\mathit{DN}_{ij}'-I_{bg,ij}\ \left[R\right]$](img458.png) |
(4.15) |
In this equation, 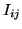 is the calibrated pixel-value,
and
is the calibrated pixel-value,
and 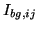 is the sky background correction.
is the sky background correction.
Removing the background
Different schemes are employed to remove the sky background in
Equation 4.15, depending on available data and the measurement
situation. Therefore background removal is only outlined here.
In the case of HF pump-enhanced aurora, linear interpolation with time
is sometimes used. Also a polynomial could be fitted line by line on
each side of the emission region. In the most recent papers
(Section 6.4) weighted sums of keograms through the emission region
and on the side of it are used. This is done under the assumption that
there is no aurora.
Regarding PSC studies (Section 6.6.1), brute-force median/min. filtering
was applied [Enell, 2002].
For general auroral studies, background determinations are extremely
difficult, as there is always some diffuse aurora present. In this
case background images must be obtained by using a filter for a
wavelength region with no auroral emissions. For the ALIS imagers,
background filters are available: 5100 Å and 6230 Å. However these
filters have seldom been used as they are only present at some
stations (Section 3.5). For the future, permanent background
photometers might be a solution of the problem.
The absolute calibration has been found to scale accurately with the
binning factors, thus:
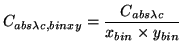 |
(4.16) |
Where
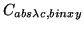 is the absolute calibration constant with binned
pixels,
is the absolute calibration constant with binned
pixels, 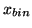 is the binning-factor
in the x-direction,
is the binning-factor
in the x-direction, 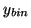 is the binning factor in
the y-direction.
is the binning factor in
the y-direction.
As no variable light-standard is available, the linearity has been
checked by varying the integration time (
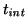 ). As
expected, the CCD detector appears to be completely linear until
it reaches the saturation-equivalent exposure (Section 3.1.10).
). As
expected, the CCD detector appears to be completely linear until
it reaches the saturation-equivalent exposure (Section 3.1.10).
Interference filters
Both the transmission characteristics and passband of a narrow-band
interference filter are subject to aging effects. The filter-wheels of
the ALIS imagers are also sometimes subject to high temperatures due
to day-time sunlight. This is known to have a permanent degenerative
effect on the filters. Questions have therefore been raised
regarding the long-term stability of the filters. To clarify these
issues, it would be desirable to re-measure filter characteristics
for the filters. This was planned for the autumn of 2001,
but had to be postponed for a number of reasons.
Another concern is to measure the transmittance of the
filter,
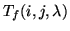 , as a function of pixel
indices,
, as a function of pixel
indices, 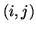 , (columns, lines). A monochromator system for
filter transmission measurements was developed for ALIS
[Vaattovaara and Enback, 1993]. Provided that an ALIS imager has a valid
flat-field calibration, it should in principle be possible to check
the transmittance of the optical system (including the filter) as a
function of wavelength and pixel coordinates. Such a study would be
beneficial for all optical instruments, using interference filters,
and could provide answers to questions posed by Kaila and Holma [2000]
regarding absolute calibration of wide field-of-view photometers and
camera systems.
, (columns, lines). A monochromator system for
filter transmission measurements was developed for ALIS
[Vaattovaara and Enback, 1993]. Provided that an ALIS imager has a valid
flat-field calibration, it should in principle be possible to check
the transmittance of the optical system (including the filter) as a
function of wavelength and pixel coordinates. Such a study would be
beneficial for all optical instruments, using interference filters,
and could provide answers to questions posed by Kaila and Holma [2000]
regarding absolute calibration of wide field-of-view photometers and
camera systems.




Next: Geometrical calibration
Up: Calibrating ALIS
Previous: Removing the instrument signature
Contents
Index
copyright Urban Brändström
![\includegraphics[]{eps/calibration/calibrators_bw.eps}](img412.png)
![\includegraphics[]{eps/calibration/calibrators_bw.eps}](img412.png)
![\includegraphics[width=\textwidth]{eps/octave/calplot.eps}](img413.png)
![]() :
:
![]() , which
is obtained from a light-standard by integrating over the
filter passband,
, which
is obtained from a light-standard by integrating over the
filter passband,
![]() is
given by:
is
given by:
![]() ,
,
![]() and
and
![]() ). Due to the
difficulties of determining these functions as well as the
approximations and uncertainties related to the
). Due to the
difficulties of determining these functions as well as the
approximations and uncertainties related to the ![]() Equation 4.9 is
rewritten as follows:
Equation 4.9 is
rewritten as follows:
![\includegraphics[]{eps/calibration/5590cal.eps}](img447.png)
![]() between the two instruments [Sergienko, 2003]. This comparison
as well as extrapolated values have been in use for the filter/imager
combinations not appearing in Table 4.5 (i.e.
ccdcam6. See also Tables 3.4 and
3.5).
between the two instruments [Sergienko, 2003]. This comparison
as well as extrapolated values have been in use for the filter/imager
combinations not appearing in Table 4.5 (i.e.
ccdcam6. See also Tables 3.4 and
3.5).
![]() is often regarded as acceptable. The
largest errors appear to be related to the intercalibration of the
light-standards (about 10-20 %, refer to Table 4.4).
Furthermore, the calibration results appear to be fairly stable over one
year (Table 4.5). On the other hand there are still many
uncertain factors in the calibration procedure, most notably the
absence of a uniform source needed for the flat-field calibration
(Section 4.1.3). Therefore, to be on the safe side, it might be
stated that the absolute calibration error lies in the range of
25-50 %. The intercalibration error of the ALIS imagers is probably
much lower, at least for pixels in the central region of the image.
For an imaging instrument, these errors are probably to be considered
as acceptable. However improvements are still required.
is often regarded as acceptable. The
largest errors appear to be related to the intercalibration of the
light-standards (about 10-20 %, refer to Table 4.4).
Furthermore, the calibration results appear to be fairly stable over one
year (Table 4.5). On the other hand there are still many
uncertain factors in the calibration procedure, most notably the
absence of a uniform source needed for the flat-field calibration
(Section 4.1.3). Therefore, to be on the safe side, it might be
stated that the absolute calibration error lies in the range of
25-50 %. The intercalibration error of the ALIS imagers is probably
much lower, at least for pixels in the central region of the image.
For an imaging instrument, these errors are probably to be considered
as acceptable. However improvements are still required.
![]() , see Equations 4.5 and 4.6):
, see Equations 4.5 and 4.6):
![]() , as a function of pixel
indices,
, as a function of pixel
indices, ![]() , (columns, lines). A monochromator system for
filter transmission measurements was developed for ALIS
[Vaattovaara and Enback, 1993]. Provided that an ALIS imager has a valid
flat-field calibration, it should in principle be possible to check
the transmittance of the optical system (including the filter) as a
function of wavelength and pixel coordinates. Such a study would be
beneficial for all optical instruments, using interference filters,
and could provide answers to questions posed by Kaila and Holma [2000]
regarding absolute calibration of wide field-of-view photometers and
camera systems.
, (columns, lines). A monochromator system for
filter transmission measurements was developed for ALIS
[Vaattovaara and Enback, 1993]. Provided that an ALIS imager has a valid
flat-field calibration, it should in principle be possible to check
the transmittance of the optical system (including the filter) as a
function of wavelength and pixel coordinates. Such a study would be
beneficial for all optical instruments, using interference filters,
and could provide answers to questions posed by Kaila and Holma [2000]
regarding absolute calibration of wide field-of-view photometers and
camera systems.