



Next: Intercalibration
Up: Calibrating ALIS
Previous: Calibrating ALIS
Contents
Index
Subsections
Removing the instrument signature
First it is necessary to remove the instrument signature from the
image data. This task is sometime called ``data reduction''. The
procedure is to a large extent similar to that followed when reducing
astronomical CCD image data [for example Massey, 1992].
In most cases the reduction is carried out first by removing additive
effects, and then proceeding with multiplicative effects.
Bias removal
The simplest way to remove the bias is to subtract an image obtained
with zero integration time (usually called bias-frame or
zero-exposure). However as the bias-frame is subject to the
same read noise (Section 3.1.7) as the object-image, this will
generally increase the noise by a factor of 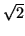 . Preparing a
bias-correction image by averaging many bias-frames together
reduces this problem. As the bias varies over time it would severely
impair the temporal resolution if a large number of zero exposures
needed to be taken at regular intervals. To remedy this most CCDs
are equipped with some extra pixels at the edge of each line. These pixels
are shaded from light and thus provide bias information for each line
for each image read-out. In the case of the ALIS imager, there are
bias-pixels (also called reference pixels, or
overscan-strip) for each line of each quadrant on the CCD as
indicated in Figure 4.1.
. Preparing a
bias-correction image by averaging many bias-frames together
reduces this problem. As the bias varies over time it would severely
impair the temporal resolution if a large number of zero exposures
needed to be taken at regular intervals. To remedy this most CCDs
are equipped with some extra pixels at the edge of each line. These pixels
are shaded from light and thus provide bias information for each line
for each image read-out. In the case of the ALIS imager, there are
bias-pixels (also called reference pixels, or
overscan-strip) for each line of each quadrant on the CCD as
indicated in Figure 4.1.
For each pixel, the bias (or
DC-level),
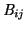 , can be expressed as follows:
, can be expressed as follows:
![$\displaystyle \mathit{B}_{ij}=\mathit{B}_{Lj}+\mathit{B}_{\overline{Z}ij}+\mathit{B}_{q}+\mathit{B}_{0}\ \left[\mathrm{counts}\right]$](img384.png) |
(4.1) |
Here
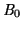 is the black-level (or preset bias), as
given in Table 4.1. This value is set in the CCD configuration
is the black-level (or preset bias), as
given in Table 4.1. This value is set in the CCD configuration
Table 4.1:
Preset bias-levels (black-levels) for the ALIS imagers. The values are obtained from the configuration files for the imagers.
| ccdcam |
Preset bias 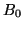 |
| 1 |
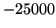 |
| 2 |
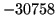 |
| 3-4 |
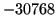 |
| 5-6 |
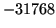 |
|
file (Section 3.3.3).
Bias variations between the four read-out channels can be equalised by
subtracting the quadrant bias,
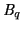 , for
each quadrant (
, for
each quadrant (
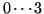 ). This value can be found by averaging
pixels from either zero exposure or from the bias-pixels.
). This value can be found by averaging
pixels from either zero exposure or from the bias-pixels.
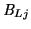 is the overscan-strip correction, which is
obtained by selecting good bias-pixels (not all are usable) and
averaging them together on each line. The number of bias-pixels varies
between the CCDs, as indicated in Table 4.2.
is the overscan-strip correction, which is
obtained by selecting good bias-pixels (not all are usable) and
averaging them together on each line. The number of bias-pixels varies
between the CCDs, as indicated in Table 4.2.
Table 4.2:
Total number of pixels and bias-pixels for the six ALIS imagers.
The bias-pixels are given per quadrant.
The number of imaging pixels is
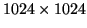 for all six CCDs.
for all six CCDs.
| ccdcam |
Total pixels (
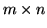 ) ) |
Bias-pixels |
| 1-4 |
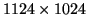 |
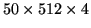 |
| 5 |
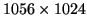 |
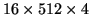 |
| 6 |
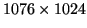 |
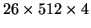 |
|
The number of usable bias-pixels varies even more. A suitable smooth
function can then be fitted to this averaged bias-column, although
this is not done in the current version of the software.
As mentioned initially, to further enhance the bias removal, it is
also possible to obtain 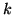 bias-frames (Typically at least 25
images), resulting in an averaged bias-correction
image,
bias-frames (Typically at least 25
images), resulting in an averaged bias-correction
image,
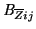 .
.
![$\displaystyle \forall(i,j) :\ \mathit{B}_{\overline{Z}ij}= \frac{1}{k}\sum_{1}^...
...it{B}_{Lj}-\mathit{B}_{q}-\mathit{B}_{0} \right) \ \left[\mathrm{counts}\right]$](img399.png) |
(4.2) |
This correction is normally only present when calibrating the imagers.
Dark-current
Correction for the dark-current is performed by taking several
dark-exposures, i.e. long exposures (
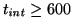 s) with the
shutter closed. The dark-current correction
image,
s) with the
shutter closed. The dark-current correction
image,
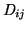 , is then produced by averaging these
images together in much the same way as the averaged bias-correction image
(Equation 4.2):
, is then produced by averaging these
images together in much the same way as the averaged bias-correction image
(Equation 4.2):
![$\displaystyle \forall(i,j) :\ \mathit{D}_{ij}= \frac{1}{k}\sum_{1}^{k}\frac{1}{...
...thit{B}_{Lj}-\mathit{B}_{q}-\mathit{B}_{0}\right)\ \left[\mathrm{counts}\right]$](img403.png) |
(4.3) |
Here 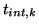 is the integration time for image
is the integration time for image 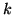 .
.
However for the ALIS imagers, this correction has been found to be
negligible for integration times less than 10-15 minutes. Therefore,
no dark-current correction is made except for very special cases.
Flat-field correction
The purpose of the flat-field calibration is to remove multiplicative
variations introduced by pixel-to-pixel sensitivity differences,
vignetting in the optics, variation in transmittance on the filter
surface, etc.. This is done by taking a large number of images of a
uniform flat-field source:
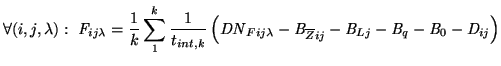 |
(4.4) |
In this equation
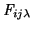 is the flat-field
correction. The
index,
is the flat-field
correction. The
index, 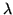 , indicates that the flat-field
correction images should be obtained for each wavelength of interest.
Normally this means one set of flat-field images per filter. However a
calibration facility which can take measurements for several
wavelengths within the filter passband would enable measurements of
the combined effects of transmittances (Section 3.1.3) and quantum
efficiency (Section 3.1.6) for the entire imaging system (and as a
function of wavelength).
, indicates that the flat-field
correction images should be obtained for each wavelength of interest.
Normally this means one set of flat-field images per filter. However a
calibration facility which can take measurements for several
wavelengths within the filter passband would enable measurements of
the combined effects of transmittances (Section 3.1.3) and quantum
efficiency (Section 3.1.6) for the entire imaging system (and as a
function of wavelength).
The moderate fields-of-view (
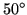 -
-
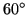 ) for the ALIS imagers
necessitate an integrating sphere of a sufficient diameter
for flat-field calibration [i.e. about 1.5-2 m, see Labsphere, 1997; Brändström, 2000, and
references therein.].
) for the ALIS imagers
necessitate an integrating sphere of a sufficient diameter
for flat-field calibration [i.e. about 1.5-2 m, see Labsphere, 1997; Brändström, 2000, and
references therein.].
Numerous attempts were made to use simpler methods, such as cloudy
skies, white screens, diffuse spherical lamp covers etc. to obtain
reasonably good flat-field images. None of these attempts provided
flat-field images of sufficient quality, as non-uniformities and
gradients were hard to avoid with these simple approaches.
One ALIS imager (ccdcam6) has actually been calibrated in the
integrating sphere facility at National Institute of Polar Research,
Japan [Okano et al., 1997]. The results from this calibration (using
white light) are described by Urashima et al. [1999]. Due to the
considerable distance to this facility it would be difficult to
perform flat-field calibrations for all cameras, as would be required.
Therefore it is hoped that a similar calibration facility will be
established in the proximity of the optical instruments in northern
Scandinavia. This was proposed by Steen [1998]. Such a facility
would be beneficial to many imaging devices in Europe.
So far no proper flat-field calibration are done on the ALIS images on
a regular basis. Instead, the flat-field correction is solely based on
a mathematical model of the vignetting in the optical system
[Gustavsson, 2000, Chapter 5]. (This model resembles the
``natural vignetting'' of
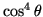 discussed in
Section 3.1.3). Despite the fact that this model does not take
variations in filter-transmission, pixel-to-pixel sensitivity
variations, etc. into account, it has proved to work reasonably well.
discussed in
Section 3.1.3). Despite the fact that this model does not take
variations in filter-transmission, pixel-to-pixel sensitivity
variations, etc. into account, it has proved to work reasonably well.
Defects are unavoidable in the production of a CCD, so
defect-free chips are extremely rare and expensive. The CCDs used for
the ALIS imagers are of scientific grade, allowing for only a few
pixel-defects. The pixel-defects, and how to detect them, can be
summarised as follows [after Holst, 1998]:
- Point defect:
- Pixel with deviation of more than 6 % compared to
adjacent pixels when illuminated to 70 % saturation. (Expose a
white area to about 70 % of the dynamic range.)
- Hot point defect:
- Pixels with extremely high output voltage.
Typically a pixel whose dark-current is 10 times higher than the
average dark-current. (Take a zero or dark image.)
- Dead pixels:
- Pixels with low output voltage and/or poor responsitivity.
Typically a pixel whose output is one half of the others when the
background nearly fills the wells. (Expose a white area.)
- Pixel traps:
- A trap interferes with the charge transfer process
and results in either a partial or whole bad line, either all
white or all dark. (Take a zero, dark or object image, depending on
type of trap)
- Column defect:
- Many (typically 10 or more) point defects in a single
column. May be caused by pixel traps (see above).
- Cluster defect:
- A cluster (grouping) of pixels with point defects
(see above).
Although the CCDs in the ALIS imager are of scientific grade, there
are a few pixel-defects present on each CCD. These defects have been
identified by manually inspecting the images. The bad pixels are then
removed by substituting interpolated values from adjacent pixels.
The corrections discussed above (apart from the bad-pixel
interpolation) are summarised in the following equation:
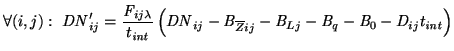 |
(4.5) |
Here,
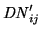 is the corrected pixel value, which
is normalised with respect to integration time
is the corrected pixel value, which
is normalised with respect to integration time
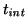 .
.
For most measurements, the following, simplified correction is applied
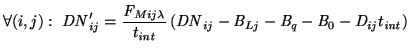 |
(4.6) |
The symbol,
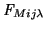 is the modelled flat-field
correction, as discussed in
Section 4.1.3.
is the modelled flat-field
correction, as discussed in
Section 4.1.3.
Apart from the steps described above, occasionally some additional
steps are carried out in order to prepare the data for subsequent
analysis. These include various types of filtering to remove
cosmic-ray events, stars, etc.




Next: Intercalibration
Up: Calibrating ALIS
Previous: Calibrating ALIS
Contents
Index
copyright Urban Brändström
![]() , can be expressed as follows:
, can be expressed as follows:
![]() is the black-level (or preset bias), as
given in Table 4.1. This value is set in the CCD configuration
is the black-level (or preset bias), as
given in Table 4.1. This value is set in the CCD configuration
![]() , for
each quadrant (
, for
each quadrant (
![]() ). This value can be found by averaging
pixels from either zero exposure or from the bias-pixels.
). This value can be found by averaging
pixels from either zero exposure or from the bias-pixels.
![]() is the overscan-strip correction, which is
obtained by selecting good bias-pixels (not all are usable) and
averaging them together on each line. The number of bias-pixels varies
between the CCDs, as indicated in Table 4.2.
is the overscan-strip correction, which is
obtained by selecting good bias-pixels (not all are usable) and
averaging them together on each line. The number of bias-pixels varies
between the CCDs, as indicated in Table 4.2.
![]() bias-frames (Typically at least 25
images), resulting in an averaged bias-correction
image,
bias-frames (Typically at least 25
images), resulting in an averaged bias-correction
image,
![]() .
.
![]() -
-
![]() ) for the ALIS imagers
necessitate an integrating sphere of a sufficient diameter
for flat-field calibration [i.e. about 1.5-2 m, see Labsphere, 1997; Brändström, 2000, and
references therein.].
) for the ALIS imagers
necessitate an integrating sphere of a sufficient diameter
for flat-field calibration [i.e. about 1.5-2 m, see Labsphere, 1997; Brändström, 2000, and
references therein.].
![]() discussed in
Section 3.1.3). Despite the fact that this model does not take
variations in filter-transmission, pixel-to-pixel sensitivity
variations, etc. into account, it has proved to work reasonably well.
discussed in
Section 3.1.3). Despite the fact that this model does not take
variations in filter-transmission, pixel-to-pixel sensitivity
variations, etc. into account, it has proved to work reasonably well.