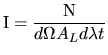
Next: Voxel Pixel Up: thesis Previous: Evaluation Contents
The Forward model - the imaging process
``It is no use saying `We are doing our best.' You have got to succeed in doing what is necessary.'' - Winston Churchill
In order to make quantitative data analysis possible it is necessary to know the absolute scale of the instrument.
For single station imaging it is sufficient to calculate the absolute
sensitivity, i.e. the number of photons needed inside the
field-of-view of the pixel on the front lens in order to create one
count in the image. The primary measurable in imaging is raw
counts. With knowledge of the number of photons per count, the
effective area of the camera and the pixel field-of-view, it is
possible to convert the raw counts to a surface brightness, defined as
photons per solid angle per area per time
![]() . For aeronomic studies it is of more
immediate interest to know the total emission from the atmosphere of the
spectral features. This conversion from surface brightness is simple
provided that the emission is isotropic and not self absorbed. If
. For aeronomic studies it is of more
immediate interest to know the total emission from the atmosphere of the
spectral features. This conversion from surface brightness is simple
provided that the emission is isotropic and not self absorbed. If
![]() photons have been detected in a pixel with a field-of-view
photons have been detected in a pixel with a field-of-view
![]() and an effective area
and an effective area ![]() , an exposure time
, an exposure time
![]() and wavelength band
and wavelength band ![]() , the corresponding surface
brightness is:
, the corresponding surface
brightness is:
This corresponds to the total number of photons emitted from a column with unit area in the direction of the pixel line-of-sight. Assuming that the emission is isotropic, the total number of photons emitted in all directions is:
In aeronomy the unit for column emission rate has been given the name
Rayleigh,
![]() ( Hunten et al., 1956).
( Hunten et al., 1956).
For an imaging system intended for tomographic inversion it is necessary to know what fraction of photons emitted in a voxel creates a count in a pixel in the image.
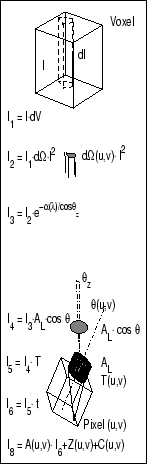 Factors which need to to be taken into account are:
Factors which need to to be taken into account are:
Voxel - pixel field-of-view intersection
For all inverse problems in this work there is a voxel
representation of the distribution of emission. To calculate the
contribution to the image intensity in one pixel from a voxel, the
intersection volume, ![]() , between the pixel field-of-view and the
voxel must be calculated. This is described in
section 5.1.
, between the pixel field-of-view and the
voxel must be calculated. This is described in
section 5.1.
Pixel field-of-view
The pixel field-of-view ![]() is solely dependent on
the optical characteristics of the camera. A general and
straightforward way to calculate this is described in
section 5.2.
is solely dependent on
the optical characteristics of the camera. A general and
straightforward way to calculate this is described in
section 5.2.
Atmospheric absorption
The light from the aurora and airglow is absorbed in the lower
atmosphere, mainly in the stratosphere. This absorption depends
on both zenith angle, ![]() , and wavelength,
, and wavelength, ![]() . This
is described in section 5.3.
. This
is described in section 5.3.
Effective collecting area
The effective collecting area of the optical system is essentially the size of the front lens as seen from the direction of the voxel. Further the limiting aperture of the optics might change with the angle relative the optical axis. This is described in section 5.4.
Transmission of optics
Variation of the transmission of the optical system with angle relative to the optical axis should be accounted for, as described in section 5.5.
Variation in exposure time
The exposure time varies slightly from pixel to pixel due to the working of the shutters; a first order correction for this is described in section 5.6.
Point spread function
The point spread functions (PSF) must be determined. The PSF is the image of a point source. The procedure for determining the PSF is outlined in section 5.7.
Pixel sensitivity
The sensitivity of individual pixels must be determined; the necessary requirements are outlined in section 5.8.
Subsections
- Voxel -- Pixel field-of-view intersection
- Pixel field-of-view
- Atmospheric absorption
- Effective collecting area
- Transmission of the optics
- Shutter characteristics
- Point spread function
- Pixel sensitivity
- Summary
Next: Voxel Pixel Up: thesis Previous: Evaluation Contents
copyright Björn Gustavsson 2000-10-24