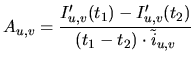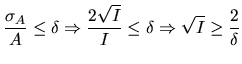
Next: Summary Up: The Forward model - Previous: Point spread function Contents
Pixel sensitivity
The basic assumption for this analysis is that the camera has an
unintensified CCD-detector giving a linear response to both photon
intensity and total number of photons. From this assumption it
follows that the detected intensity depends linearly on both the total
number of photons and the intensity. Thus, provided that no
non-linearities are added (Brändström private communication), the
output from the pixel with image coordinates ![]() is:
is:
where
To calibrate the camera the first step is to make a large series of
images with zero time of exposure to get as good an estimate as
possible of ![]() . The second step is to take a large number of
images without any light to estimate the dark current
. The second step is to take a large number of
images without any light to estimate the dark current
![]() ;
this has been done with sufficient accuracy for the ALIS cameras.
;
this has been done with sufficient accuracy for the ALIS cameras.
When the zero level and dark current is determined it is possible to rewrite equation (5.18):
where
where
If the requirement on the accuracy of the sensitivity estimate is a relative error of
This infers that if the accuracy requirements on the sensitivity is
Next: Summary Up: The Forward model - Previous: Point spread function Contents
copyright Björn Gustavsson 2000-10-24