Next: Pixel field-of-view Up: The Forward model - Previous: The Forward model - Contents
Voxel -- Pixel field-of-view intersection
In order to calculate the contribution from a voxel to a pixel in an
image, the volume of the intersection between the pixel field-of-view
and the voxel has to be calculated. The intersection between a voxel
and the pixel field-of-view is a body with between four and ten
faces. In order to avoid having to calculate the volume of the
complex body with all its bounding planes, the intersection volume
![]() is approximated by the area spanned by the pixel field-of-view,
is approximated by the area spanned by the pixel field-of-view,
![]() , at distance,
, at distance, ![]() , to the voxel
multiplied by the pixel line-of-sight intersection length
, to the voxel
multiplied by the pixel line-of-sight intersection length ![]() :
:
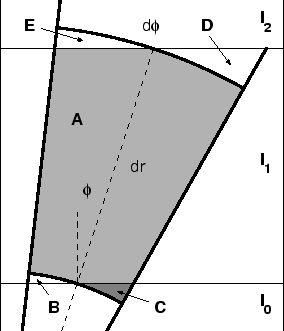
In order to study the error in the approximation, we turn to the corresponding two-dimensional example illustrated in figure 5.2. The manageable problem is a narrow circle sector intersecting three voxels with intensities
| (5.4) | ||
| (5.5) |
Where
The true contribution from voxel 1 is
| (5.6) | ||
| (5.7) |
Calculating the difference between the true and the approximate contribution, and using equations (5.4 and 5.5), gives:
After doing some geometry and some algebra the areas of the different regions can be obtained:
| (5.9) | ||
| (5.10) | ||
| (5.11) | ||
| (5.12) |
Substituting these equations into equation (5.8) and expanding to the third order in
Here it is seen that the approximate contribution,
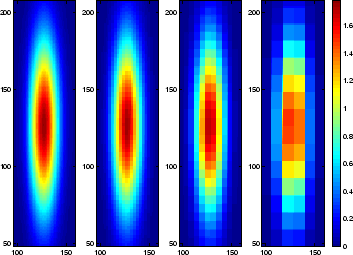
As proven the approximation for voxel-pixel intersection is good enough. A significantly more interesting topic is whether or not the voxel approximation of the continuous volume emission distribution is good enough. As a first test a simple model with only 1 voxel in altitude and a 2-D Gaussian intensity distribution is used with various sizes of the voxels. These voxel representations are projected down onto images with 256 by 256 pixels as shown in figure 5.3.
 |
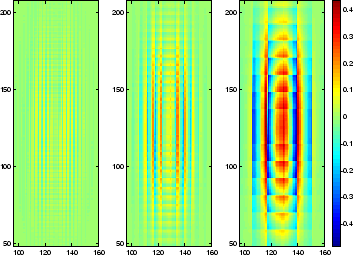 |
Next: Pixel field-of-view Up: The Forward model - Previous: The Forward model - Contents
copyright Björn Gustavsson 2000-10-24