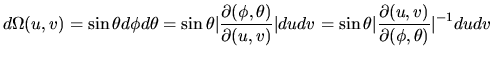
Next: Atmospheric absorption Up: The Forward model - Previous: Voxel Pixel Contents
Pixel field-of-view
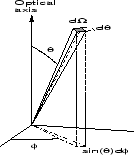
In order to calculate the approximate intersection volume of the voxel in equation (5.3), the pixel field-of-view must be calculated.
Once the parameters of the optical transfer
function are determined as outlined in chapter 4, the pixel
field-of-view, ![]() , can be determined by standard calculus. With
, can be determined by standard calculus. With
![]() as the angle relative to the optical axis of the camera, and
as the angle relative to the optical axis of the camera, and
![]() as the azimuthal angle, the field-of-view is calculated as:
as the azimuthal angle, the field-of-view is calculated as:
for which
copyright Björn Gustavsson 2000-10-24