Modelling of the emissions To model the spatial distribution and temporal variation of the emissions it is necessary to model accurately the contribution from the different sources. Since there are both direct electron excitation of the excited states and chemical sources with temperature dependent reaction rates, a model of the emission must account for the chemistry and thermodynamics of the thermosphere as well as the altitude and energy variations of the energetic electron flux. To do this it is necessary to solve the continuity equations of the minor neutral species $(O(^1D), O(^1S), N(^4S), N(^2P), N(^2D), N(^2P), NO)$ and the ions $O_2^+, NO^+, N_2^+, O^+$ in order to obtain the time- and altitude-dependent variations in the ionosphere-thermosphere system. Further it is necessary to solve the neutral, ion, and electron energy equations in order to obtain the variations in the temperatures. In order to take the electron excitation into account it is also necessary to model the electron transport and production of secondary electrons. This gives a coupled set of non-linear partial differential equations which must be solved simultaneously. Precipitating electrons ionize the atmosphere along their trajectories, creating secondary electrons with lower energies. This process increases the electron and ion concentrations and, moreover, leads to heating of the ions and ambient electrons through energy dissipation. From the ion-neutral collisions the neutral atmosphere is heated, the change in the temperatures influence the chemistry that affects the recombination rates of electrons and ions. The electron transport alone is a complicated process -- expressed by a continuity equation taking into account discrete and continuous energy loss processes, scattering of energetic electrons and production of secondary electrons by ionization. A more detailed description of this interesting and challenging science is outside the scope of this thesis. Several ionosphere-thermosphere-electron-transport models exist in the scientific community. The following list of references is intended to be neither complete nor fair, but should rather be seen as a set of starting points for reading: An exhaustive overview of the factors that influence the auroral ionosphere-thermosphere is given by Roble and Rees (1977). A detailed electron transport code is presented by Lummerzheim and Lilensten (1994). A coupled electron-hydrogen-proton transport model including the effects of proton precipitation is reported and used by Basu et al. (1993) and Strickland et al. (1993). A pseudo three-dimensional model for the ionosphere is the USU (Utah State Univ.) time-dependent ionospheric model (TDIM) in which the one-dimensional ion and electron continuity equations are solved as functions of height for convecting flux tubes ( Schunk, 1988). Solomon et al. (1988) and Hill et al. (2000) present work based on a model of one-dimensional electron transport coupled to the chemistry. The electron transport problem has been solved with Monte Carlo methods by e.g. Ivanov and Sergienko (1992). The ionospheric modeling has been used to derive methods to make estimates of the characteristics of the precipitating particles from optical observations. Rees and Luckey (1974) derived relations between the intensities of the emissions in 5577 Å, 4278 Å and 6300 Å and the total fluxes and characteristic energies of the precipitating electrons. Strickland et al. (1989) addressed the problem of variability in oxygen density and suggested an improved method which derived electron characteristics and oxygen scaling factors from ratios of the emissions at 4278 Å, 6300 Å and 7444 Å. This method was then extended to use the 8446 Å emission instead of the 7444 Å. Use of the 6300 Å emission requires stable conditions to give reliable results, because of the long effective lifetime of $O(^1D)$. Rapid variations in precipitation give rapid changes in the emissions in the other wavelengths but the 6300 Å emission is smoothed. Further, the altitude distribution of the emission depends on the characteristic energy of the precipitating electrons. This has been used to derive characteristics of the precipitating electrons e.g. Aso et al. (1998a). Since the $O(^1S)$ state has several sources (c.f. section 2.1), the retrieval of the spectra of the primary electrons is impaired by uncertainties that are difficult to overcome. Retrieval of the primary electron spectra from an emission with only one signifficant source such as 4278 Å is a simpler problem. If we use the experimentally derived electron transport relations presented in Rees (1989) with energy deposition, scattering depth, effective range, and an average energy loss per ionization, the retrieval of the primary spectra becomes a linear inverse problem if we assume that 2.13 % of the $N_2$ ionization leads to emission in 4278 Å. The emission caused by a mono-energetic electron beam with energy $E_p$ in $I(4278)$ in 4278 Å at altitude $z$ is given by: $$\begin{split}I(4278,z) = &\frac{0.0213}{\Delta\epsilon_{ion}}... ..._2}(z)}{0.92\,n_{N_2}(z)+n_{O_2}(z)+0.56\,n_{O}(z)} \end{split}$$ (2.17) Here $n_X(z)$ is the concentration of specie $X$, $\Delta\epsilon_{ion}$ is the average energy loss per ionization, $F$ is the electron flux, $\Lambda(s/R)$ is the energy dissipation function (presented in Figure 2.2), $\rho(z)$ is the Figure 2.2: Energy dissipation distribution function for unidirectional electrons. Normalized to conserve energy, $\int_{-1}^{1}\Lambda(\frac{s}{R})d\frac{s}{R}\equiv 1$. Data from Figure 3.3.2 in Rees (1989). mass density (obtained from atmosphere models such as MSIS Hedin (1991)), $R(E_p)$ is the effective range: $$R(E_p) = 4.3\cdot10^{-7}+5.36\cdot10^{-6}\,E_p^{1.67}$$ (2.18) where $R$ is in gm$\,$cm$^{-2}$ and the electron energy $E_p$ is in keV. The scattering depth $s$ is given by: $$s(z) = \int^\infty_z\rho(z)dz$$ (2.19) Figure 2.3: Altitude profiles of the 4278 Å emission rate due to an incident electron flux of $10^8$ electrons cm$^{-2}$s$^{-1}$ for different initial energies. 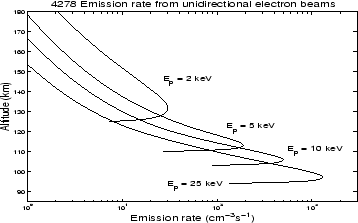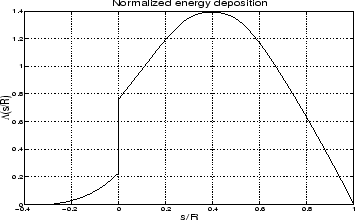With increasing incident electron energy the altitude variation of the emission changes to peak at lower altitudes with decreasing widths, as shown in Figure 2.3. In paper II this method was used to determine the incident electron spectra for a 20 minute event with a stable auroral arc.