Next: Tomography Up: Aurora and artificial airglow Previous: Modelling of the emissions Contents
Artificial airglow
It is possible to enhance the natural airglow by transmitting a high power high frequency (HF) radio beam that modifies the ionosphere when the ionospheric conditions are favourable (i.e. high enough electron concentration and at high latitudes little or no auroral activity). The enhanced airglow is far too weak to be visible by the unaided eye but it is detectable from the ground with sensitive imagers and photometers. This section gives a very short introduction to the phenomenon of artificially enhanced airglow.
When a powerful HF-beam is transmitted into the ionosphere a number of wave-wave and wave-particle interactions might occur. Here these processes are only mentioned as an intermediate step in the energy transfer from the radio wave to the excitation of the atoms and molecules which emit the enhanced airglow.
 |
When the O-mode radio wave propagates into the ionosphere it is
reflected at the altitude at which its frequency equals the local
plasma frequency. In the region just below the reflection altitude the
amplitude of the E-field of the radio wave swells and rotates from
transverse to parallel to the magnetic field. This creates strong
wave-wave and wave-particle interactions known as Langmuir
turbulence. It has been shown that this creates supra-thermal
electrons, theoretically by e.g. Weinstock and Bezzerides (1974); Gurevich et al. (1985); Perkins and Kaw (1971); Weinstock (1975) and Wang et al. (1997), and
experimentally by e.g. Carlson et al. (1982) and
Fejer and Sulzer (1987). This is the dominant dissipation mechanism at
mid latitudes, such as for Arecibo, where a vertically transmitted
pump wave propagates at about 40 to the local magnetic field. At
high latitudes, such as for northern Scandinavia where the HF-wave
propagates nearly parallel to
the magnetic field, the Langmuir turbulence is present but in addition
at altitudes a few kilometres lower than the HF pump reflection
height most of the pump energy may be dissipated by the excitation of
upper hybrid turbulence. The excitation of upper hybrid turbulence is
particularly strong for pump frequencies not near an harmonic of the
ionospheric electron gyro frequency and sufficiently long pumping
(several seconds). These
interactions create striations which are density and temperature
pertubations that are elongated along the earth's magnetic field. These
structures cause anomalous absorption of the HF pump wave
( Robinson, 1989; Gurevich et al., 1996). When the Langmuir and/or upper
hybrid turbulence dissipate energy, e.g. by increasing the plasma
temperatures or accelerating electrons, a small
fraction leads to excitation of atomic oxygen to the ![]() and
and
![]() states thus causing enhancements in the 6300 and 5577 Å
airglow.
states thus causing enhancements in the 6300 and 5577 Å
airglow.
Several mechanisms have been proposed to explain the enhanced
airglow. There are two main theoretical models for HF-pump
enhanced airglow: one model suggests that the airglow is caused by
![]() excitation of the high energy tail of a Maxwellian electron
distribution
( Mantas and Carlson, 1996; Gurevich and Milikh, 1997; Mantas, 1994), and the
other suggests that the
excitation of the high energy tail of a Maxwellian electron
distribution
( Mantas and Carlson, 1996; Gurevich and Milikh, 1997; Mantas, 1994), and the
other suggests that the ![]() state is excited by accelerated
electrons
( Weinstock and Bezzerides, 1974; Gurevich et al., 1985; Perkins and Kaw, 1971; Weinstock, 1975).
state is excited by accelerated
electrons
( Weinstock and Bezzerides, 1974; Gurevich et al., 1985; Perkins and Kaw, 1971; Weinstock, 1975).
The only theory which quantitatively relates the enhanced airglow to
observable ionospheric parameters
![]() is the thermal theory
given by Mantas (1994). This model suggests that the
excitation of the
is the thermal theory
given by Mantas (1994). This model suggests that the
excitation of the ![]() state is caused by excitation of the
high energy tail
state is caused by excitation of the
high energy tail
![]() eV
eV![]() of a thermal/Maxwellian
electron distribution, where
of a thermal/Maxwellian
electron distribution, where
Under the assumption that the electron distribution is Maxwellian, it is possible to calculate a ``thermal excitation rate''
giving an electron impact excitation rate ( Mantas, 1994) of
where
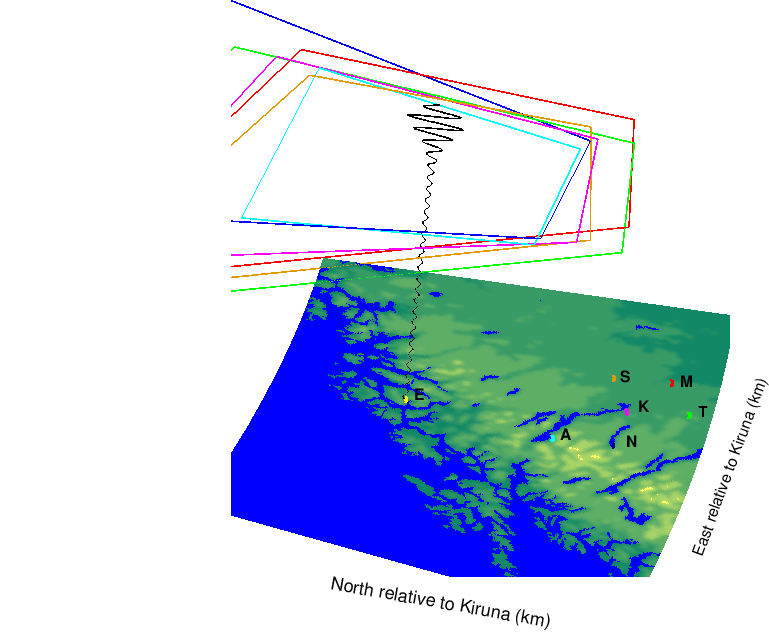
Paper IV and Paper V reports the time variation of the three-dimensional distribution of the enhanced 6300 Å airglow produced by the EISCAT-Heating facility ( Rietveld et al., 1993) near Tromsø, Norway on 16th February 1999. It is found that there are discrepancies between the predictions by the thermal model and the observations. From the EISCAT UHF radar measurements of electron temperature and electron concentration, the theoretically predicted airglow has a peak volume emission rate 15 to 20 km below the observed altitude of maximum emission. Further, the airglow enhancements are predicted to be between a factor of 2 and 3 above the natural background airglow intensity compared with the observed enhancement of 50 %. If the electron temperature measured by EISCAT is reduced so that the thermal model produces the observed enhancement of 50 %, the time variation of the airglow does not match -- the modeled airglow has a lag time from the start of the HF-pulse before the airglow intensifies. This lag time is absent in the observations.
A further shortcoming of the thermal model is that it assumes that
the electron distribution remains Maxwellian irrespective of the large
energy-dependent cross section for excitation of the neutral atoms and
molecules. For each inelastic collision one electron loses a
significant amount of energy; for excitation of the ![]() state
the energy loss is 1.96 eV, and for excitation of
state
the energy loss is 1.96 eV, and for excitation of ![]() vibrational
states the energy loss is 0.2888 eV per vibrational level. This has
been reported to produce a significant depletion of the electron
distribution function in the energy range 2 - 3 eV:
Stubbe (1981) calculated the ``modifying effects of a strong
electromagnetic wave upon a weakly ionized plasma...'' taking both the
wave-electron and electron-neutral interactions into account with
parameters typical for the ionospheric D region; for auroral
precipitation several authors have calculated significant bite-outs
in the electron flux at altitudes up to 150 km
(e.g. Rees, 1989; Konovalov et al., 1995). Bernhardt et al. (1989)
calculated the modification effect on the electron distribution
function of excitation of the vibrational states in
vibrational
states the energy loss is 0.2888 eV per vibrational level. This has
been reported to produce a significant depletion of the electron
distribution function in the energy range 2 - 3 eV:
Stubbe (1981) calculated the ``modifying effects of a strong
electromagnetic wave upon a weakly ionized plasma...'' taking both the
wave-electron and electron-neutral interactions into account with
parameters typical for the ionospheric D region; for auroral
precipitation several authors have calculated significant bite-outs
in the electron flux at altitudes up to 150 km
(e.g. Rees, 1989; Konovalov et al., 1995). Bernhardt et al. (1989)
calculated the modification effect on the electron distribution
function of excitation of the vibrational states in ![]() to be so
significant that it effectively increased the excitation threshold of
the
to be so
significant that it effectively increased the excitation threshold of
the ![]() state to 3.1 eV. In paper VI an attempt has been made to
estimate the magnitude of the electron distribution function
modification due to the electron neutral interaction. The results
indicate that at altitudes below 220 - 230 km the electron
distribution has a significant bite-out above 2 eV. This bite-out
decreases the
state to 3.1 eV. In paper VI an attempt has been made to
estimate the magnitude of the electron distribution function
modification due to the electron neutral interaction. The results
indicate that at altitudes below 220 - 230 km the electron
distribution has a significant bite-out above 2 eV. This bite-out
decreases the ![]() excitation at altitudes lower than 220 km, and
the total
excitation at altitudes lower than 220 km, and
the total ![]() excitation for typical HF enhanced electron
temperature profiles would be decreased by at least 30 %. Further it
is shown that transport effects cannot be neglected.
excitation for typical HF enhanced electron
temperature profiles would be decreased by at least 30 %. Further it
is shown that transport effects cannot be neglected.
Altogether this indicates that a complete model for HF enhanced airglow has to take electron-neutral interaction into account as well as transport effects. This level of description requires that the HF wave-plasma interaction models must produce quantitative disturbed electron distributions.
Next: Tomography Up: Aurora and artificial airglow Previous: Modelling of the emissions Contents
copyright Björn Gustavsson 2000-10-24
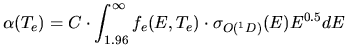
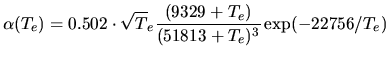 cm
cm