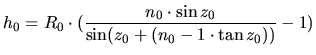
Next: Evaluation Up: Geometrical calibration of ALIS Previous: System and requirements Contents
Calibration methods
For studies of the atmosphere and the ionosphere it is appealing to use calibration images made under the same conditions with exactly the same rotations and use background stars as a way of determining the lines-of-sight. In this way the refraction of light in the atmosphere is automatically accounted for.
The requirement that the determination of the viewing directions
should be accurate to within
![]() implies that the sky positions of these stars need to be
known to within
implies that the sky positions of these stars need to be
known to within ![]() . This accuracy
requirement demands that the sky positions of the stars have to be
rigorously corrected for precession when calculated from the star
catalogue. The star catalogue used in this work is the Yale Bright
Star catalogue (YBS) which contains selected stars down to a magnitude
6. In order to verify the accuracy of the position calculations, the
results have been compared with the star chart program
xephem
(available at the time of writing in version
3.2.3). It
is not necessary to correct for the nutation, the minor variation in
the inclination of the earth axis due to the torque from the
moon. Likewise it is not necessary to include the corrections for
aberration, proper motion and parallax in the calculations. These
higher order corrections are smaller than
. This accuracy
requirement demands that the sky positions of the stars have to be
rigorously corrected for precession when calculated from the star
catalogue. The star catalogue used in this work is the Yale Bright
Star catalogue (YBS) which contains selected stars down to a magnitude
6. In order to verify the accuracy of the position calculations, the
results have been compared with the star chart program
xephem
(available at the time of writing in version
3.2.3). It
is not necessary to correct for the nutation, the minor variation in
the inclination of the earth axis due to the torque from the
moon. Likewise it is not necessary to include the corrections for
aberration, proper motion and parallax in the calculations. These
higher order corrections are smaller than ![]() .
.
To proceed with determining the pixel lines-of-sight it is necessary
to be able to identify a large number of stars in an image,
preferably more than 100 evenly distributed over the image plate. For
these ``star pixels'' we know the lines-of-sight to within the
required accuracy. For the intermediate pixels we can choose either to
interpolate between the lines-of-sight from neighbouring star pixels or use an optical
transfer function that describes where the light from a direction in
space
![]() falls on the image. The identified
stars are used to adjust the parameters of the optical transfer
function so that the calculated directions of the stars are mapped
down to their respective points on the image.
falls on the image. The identified
stars are used to adjust the parameters of the optical transfer
function so that the calculated directions of the stars are mapped
down to their respective points on the image.
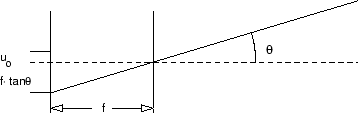
For practical work the first approximation of an optical transfer function is the pinhole camera model, which is described in most textbooks on optical imaging ( Gonzalez and Woods, 1993); see Figure 4.2. The incident light from a direction in space
| (4.4) | ||
| (4.5) |
where
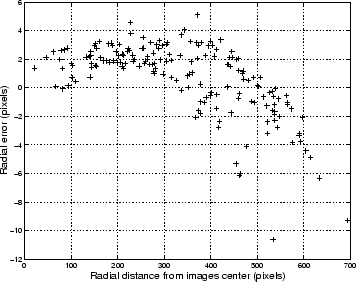 |
After a new fit of the optical parameters for the modified optical model, it appears that the systematic error has been removed (see Figure 4.4).
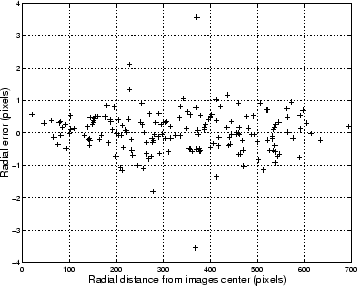 |
For the auroral and atmospheric studies which are the focus of ALIS, where the aim is to determine the position of objects at altitudes between 15 and 500 km, the required parameter is the path of the light through the atmosphere.
Due to the variations in density and temperature with altitude, the
refractive index of the atmosphere varies from 1 in free space to
approximately 1.0003 at sea level. This variation in refractive index
causes an object outside the atmosphere to appear closer to zenith than
it actually is. An everyday example of this is that
when the sun disappears from the horizon its centre is
already ![]() below the horizon.
below the horizon.
For a flat plane parallel atmosphere the total change in zenith angle is easily calculated by Snell's law:
where
This simple relation is correct to within
In order to determine the path through the atmosphere there are three choices: to use the apparent zenith angle and to perform a path tracing in order to calculate the true path of the light, to use the apparent zenith angle and assume that the light travels in a straight line, or to use the true zenith angle and use that angle for calculating the line-of-sight.
If we use the true zenith as the zenith angle of the light ray there will be an error between that ray and the true path of light due to the refraction in the atmosphere as can be seen in Figure 4.5,
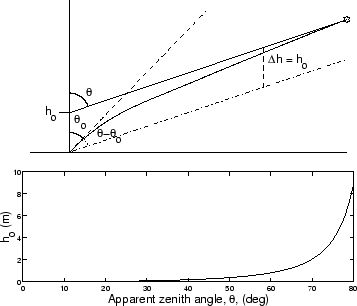 |
For zenith angles of up to
If we were to use the apparent zenith angle, the error between the infered and the true paths of light would be:
For a zenith angle of 45the difference between true and apparent zeniths is approximately 1 arc minute which gives an error of approximately 60 m at 200 km distance. Here it can be concluded that use of the true zenith angles and approximations of the light path with a straight line gives errors that are within the acceptable accuracy. The small error that results from this approximation can be compared with all other errors in the analysis and weighted against the computationally heavy and cumbersome task of performing a path-tracing through an atmosphere whose refractive index structure as a function of altitude is, at best, only roughly known.
Next: Evaluation Up: Geometrical calibration of ALIS Previous: System and requirements Contents
copyright Björn Gustavsson 2000-10-24