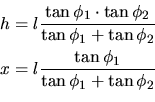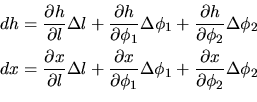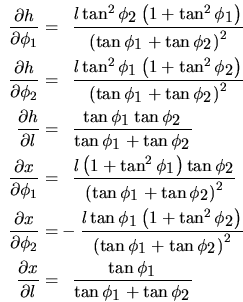
Next: Calibration methods Up: Geometrical calibration of ALIS Previous: Introduction and overview Contents
System and requirements
Currently ALIS is equipped with cameras with a resolution of 1024 by 1024 pixels and a field-of-view of approximately
A first order error analysis
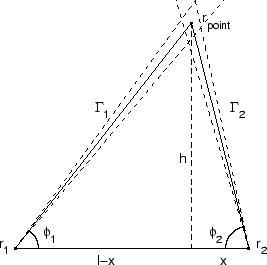
is easily accomplished if we look at stereoscopic triangulation of an
object point found in two images from sites at
![]() and
and
![]() , respectively (Figure 4.1).
, respectively (Figure 4.1).
where the parameters are defined as shown in Figure 4.1. The sensitivity of
which can be expanded by calculating the partial derivatives:
From these equations it is possible to calculate the propagation of uncertainties in the lines-of-sight to the positions for all directions. As a rule of thumb, as the station separation is small compared to the distance to the object, i.e.
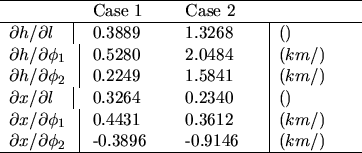
In order to estimate the orders of magnitude of the derivatives, two examples with typical values for stratospheric (case 1) and auroral (case 2) work are given in table 4.1.
As can be seen
from equation (4.2) and table 4.1, the
requirements on the parameter accuracy to obtain the estimated
distances to within 50 m are, for auroral studies, of the order of 50
m for the baseline separation, ![]() , and
, and ![]() for the
angular accuracy,
for the
angular accuracy,
![]() ; for
stratospheric studies the requirements are less strict.
; for
stratospheric studies the requirements are less strict.
Next: Calibration methods Up: Geometrical calibration of ALIS Previous: Introduction and overview Contents
copyright Björn Gustavsson 2000-10-24