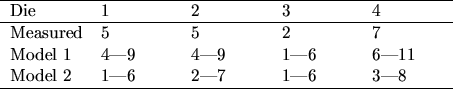
Next: Summary Up: Tomography Previous: Error sensitivity Contents
Stopping criteria
It has long been known that iterative solutions to tomographic problems improve initially but deteriorate after some point ( Gordon and Herman, 1974). This highlights the importance of knowing when it is time to stop.
What we want to do is to test whether the reconstruction gives
projections that are statistically compatible with the observed
images. If we had a large number of samples ![]() from one random
process, it is possible to test whether the random process has a
hypothetical probability distribution
from one random
process, it is possible to test whether the random process has a
hypothetical probability distribution ![]() . The method to do this
is the
. The method to do this
is the ![]() -test of fit for which the range of the random
variable is divided into
-test of fit for which the range of the random
variable is divided into ![]() intervals,
intervals, ![]() with theoretical
probabilities
with theoretical
probabilities ![]() for a random sample
for a random sample ![]() to fall into the
interval
to fall into the
interval ![]() if the hypothesis
if the hypothesis
![]() is true.
is true.
With a total of ![]() samples
samples
![]() and
and ![]() samples in
interval
samples in
interval ![]() , the
, the ![]() -test function
-test function
has an asymptotic
In the case of tomography, the pixels in the projection images of the reconstructed three-dimensional source distribution are the expected values of the probability distributions from which the measured pixel values are the random samples. Here we only have one sample from each probability distribution; it should be noted that the probability distribution for a pixel value is known and assumed to be determined only from the expected value.
For auroral imaging with ALIS, the pixel intensity has a probability
distribution that is
![]() as
derived in section 3.1. With the
above relation between expected pixel intensity and the
random distribution of the measured pixel intensity, it is possible
to use the above
as
derived in section 3.1. With the
above relation between expected pixel intensity and the
random distribution of the measured pixel intensity, it is possible
to use the above ![]() -test after the modification that the
random process for each pixel is divided into intervals with equal
probabilities
-test after the modification that the
random process for each pixel is divided into intervals with equal
probabilities ![]() and that the measured pixel intensity is put
into its corresponding interval.
and that the measured pixel intensity is put
into its corresponding interval.
The hypothesis that the measured images ![]() are random samples from
a set of random processes with expected values
are random samples from
a set of random processes with expected values
![]() is
accepted if the
is
accepted if the ![]() value calculated from
equation (3.15) is less than is required at the corresponding
significance level. (The values of
value calculated from
equation (3.15) is less than is required at the corresponding
significance level. (The values of
![]() are calculated from
the source distribution.) For processes that have continuous probability distributions, it is
no problem to divide the range into equal intervals for different
expected values and widths but for discrete probability
distributions this can be a problem; for Poissonian processes a
method to overcome this problem is described by Veklerov and Llacer (1987).
are calculated from
the source distribution.) For processes that have continuous probability distributions, it is
no problem to divide the range into equal intervals for different
expected values and widths but for discrete probability
distributions this can be a problem; for Poissonian processes a
method to overcome this problem is described by Veklerov and Llacer (1987).
An example that can illustrate the working procedure outlined above is
to look at the outcome of the roll of four non-standard dice. What
separates these dice from ordinary dice is that they have
unknown numbers of dots; that
is, they might have dots from 1 to 6 or from 3 to 8 or any other
sequence of
dots
![]() . If we make a measurement of the dot numbers
and then get two models which estimate the expected value of each
die, as presented in table 3.4, the algorithm for this
stopping criteria is as follows.
. If we make a measurement of the dot numbers
and then get two models which estimate the expected value of each
die, as presented in table 3.4, the algorithm for this
stopping criteria is as follows.
First we divide the probability distribution into a number of intervals, for this case two intervals
and for model 2 die
For a significance level of
If we have come this far the reconstruction gives projections
that fit the measured images in a statistical sense. However, there
are not yet any guarantees that the spatial distribution of the errors
is well behaved, i.e., the large positive errors might be grouped
together in one region of the images and small errors
might be grouped in another region. One further condition for
optimal reconstructions is that the spatial distribution of the
errors is also random. This can be tested with the same method as
above: the image location of errors in an intensity interval ![]() is calculated and then the images are divided into 10 by 10 regions
and the number of errors
is calculated and then the images are divided into 10 by 10 regions
and the number of errors ![]() from the interval
from the interval ![]() is
calculated region by region. If the
is
calculated region by region. If the ![]() -test function
-test function
where
By the way, about the cartoon animation on the even pages - it starts of at page 2. The images in the top right corner are ALIS data of HF enhanced airglow from Silkimuotka and the images in the lower left corner is the projected images of the retrieved volume emission. The animation starts at 17:40:15 UT with 10 s between each frame and covers about one HF-pump on-off cycle.
Next: Summary Up: Tomography Previous: Error sensitivity Contents
copyright Björn Gustavsson 2000-10-24