



Next: Selecting an imager for
Up: The ALIS Imager
Previous: The ALIS Imager
Contents
Index
Subsections
There exist a number of textbooks [for example Theuwissen, 1995; Holst, 1998, and references
therein], reports
[for example Lance and Eather, 1993; Eather, 1982], and articles
[for example Janesick et al., 1987, and references therein] on solid-state
imaging with CCD detectors. This section will provide a short summary
of some fundamental concepts required to specify a CCD-imaging system
suitable for the needs of auroral and airglow imaging.
Holst [1998] defines the term radiometry, as the
``energy or power transfer from a source to a detector''
while photometry is defined as ``the transfer
from a source to a detector where the units of radiation have been
normalised to the spectral sensitivity of the eye.''
Spectral radiant sterance (radiance)
The basic quantity from which all other radiometric quantities can be
derived is spectral radiant sterance, 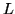 . Given a
source area,
. Given a
source area, 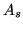 , radiating a
radiant flux,
, radiating a
radiant flux, 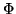 , into a solid
angle,
, into a solid
angle, 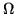 . The spectral radiant
sterance in energy units,
. The spectral radiant
sterance in energy units, 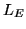 ,
then becomes:
,
then becomes:
![$\displaystyle L_{E}(\lambda)=\frac{\partial^{2}\Phi(\lambda)}{\partial A_{s}\partial\Omega}\ \left[\frac{\mathrm{W}}{\mathrm{m^2\ sr}}\right]$](img92.png) |
(3.1) |
where 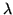 is the wavelength. Expressing the
spectral radiant sterance in quantum units (
is the wavelength. Expressing the
spectral radiant sterance in quantum units (
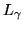 )
the following equation is obtained:
)
the following equation is obtained:
![$\displaystyle L_{\gamma}=\frac{L_{E}}{h\nu}=\frac{L_{E}\lambda}{hc}\ \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2\ sr}}\right]$](img95.png) |
(3.2) |
Here 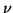 is the frequency,
is the frequency, 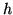 is Planck's
constant and
is Planck's
constant and 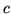 is the speed of light. Please note
spectral radiant sterance (radiance) is not to be confused with
surface brightness which is a photometric unit involving the
characteristics of the human eye [see Holst, 1998, pp.
20,26].
is the speed of light. Please note
spectral radiant sterance (radiance) is not to be confused with
surface brightness which is a photometric unit involving the
characteristics of the human eye [see Holst, 1998, pp.
20,26].
The Rayleigh
In terms of measurement techniques the aurora can be regarded as a
five-dimensional signal with three spatial dimensions, one temporal
and one spectral dimension. The desired physical quantity is usually
the volume emission rate,
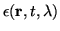 , which cannot
be found directly from measurements. However the rate of emission from
a
, which cannot
be found directly from measurements. However the rate of emission from
a
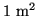 column along the line of sight is normally just
column along the line of sight is normally just
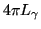 for any isotropic source with no self-absorption
[Hunten et al., 1956].
for any isotropic source with no self-absorption
[Hunten et al., 1956].
Consider a cylindrical column of cross-sectional area 1
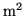 extending away from the detector into the source. The volume emission
rate from a volume element of length
extending away from the detector into the source. The volume emission
rate from a volume element of length 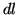 at distance
at distance 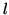 is
is
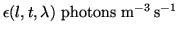 . The contribution to
. The contribution to
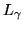 is given
by:
is given
by:
![$\displaystyle dL_{\gamma}=\frac{\epsilon(l,t,\lambda)}{4\pi}\,dl\ \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2\ sr}}\right]$](img107.png) |
(3.3) |
Integrating along the line of sight, 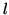 :
:
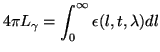 |
(3.4) |
This quantity is the column emission rate, which
Hunten et al. [1956] proposed as a radiometric unit for the
aurora and airglow. (See also Chamberlain [1995, App.
<]2058#> II#) The unit is named after the fourth
Lord Rayleigh, R. J. Strutt, 1875-1947, who made the first
measurements of night airglow [Rayleigh, 1930]. (Not to be
confused with his father, J. W. Strutt, 1842-1919 remembered for
Rayleigh-scattering etc.) In SI-units
the Rayleigh becomes [Baker and Romick, 1976]:
![$\displaystyle 1\ \mathrm{[Rayleigh]} \equiv 1\ \mathrm{[R]} \triangleq 10^{10} \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2\ column}}\right]$](img110.png) |
(3.5) |
The word column denotes the concept of an emission-rate from
a column of unspecified length, as discussed above. It should be noted
that the Rayleigh is an apparent emission rate, not taking absorption
or scattering into account. However, Hunten et al. [1956]
emphasise that ``the Rayleigh can be used as defined without
any commitment as to its physical interpretation, even though it has
been chosen to make interpretation convenient.'' The spectral
radiant sterance (
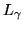 ) in Equation 3.2 can be obtained from
the column emission rate
) in Equation 3.2 can be obtained from
the column emission rate 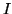 (in Rayleighs) according to
Baker and Romick [1976]:
(in Rayleighs) according to
Baker and Romick [1976]:
![$\displaystyle L_{\gamma}=\frac{10^{10}I}{4\pi} \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2\ sr}}\right]$](img112.png) |
(3.6) |
Although not a proper SI-unit, the Rayleigh is often used in the field
of auroral and airglow measurements. It is also frequently
misunderstood and abused. It is important to remember that the
Rayleigh only is usable when the wavelength is specified. Due to
the plethora of Rayleigh definitions [Baker and Romick, 1976], it is
always wise to state the definition of the unit before using it. In
the following text, the Rayleigh will be used according to the
original definition [Hunten et al., 1956, but in SI-units] as defined
above.
Using the recommended column emission rates in Rayleighs for the
International Brightness Coefficients ( IBC)
as an example, the following spectral radiant sterances are obtained
[Chamberlain, 1995, App. II]: IBC-I aurora,
corresponding to 1 kR at 5577 Å is often described as the lowest
column emission rate detectable by the unaided human eye. Usually
this is compared to the luminous incidence of a moonless cloudy night
which is about 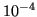 Lux3.1. By the use of Equations 3.2 and 3.6, the
spectral radiant sterance in energy units (
Lux3.1. By the use of Equations 3.2 and 3.6, the
spectral radiant sterance in energy units (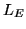 ) can be
calculated:
) can be
calculated:
![$\displaystyle L_{E}(1\ \mathrm{[kR]})=\frac{10^{13} hc}{4\pi\lambda}= \frac{10^{3}hc}{4\pi\times5577} \approx 300 \left[\frac{nW}{\mathrm{s\ m^2\ sr}}\right]$](img114.png) |
(3.7) |
Similarly the brightest IBC-IV corresponding to 1 MR at
5577 Å, which is often compared to the luminous incidence of the
full-moon of about
 Lux3.1
becomes:
Lux3.1
becomes:
![$\displaystyle L_{E}(1\ \mathrm{[MR]})\approx 300 \left[\frac{\mu W}{\mathrm{s\ m^2\ sr}}\right]$](img116.png) |
(3.8) |
Spectral radiant incidence (irradiance)
Spectral radiant incidence (irradiance), 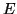 , is defined as
radiant power incident per unit area onto a target, in this case
typically the effective aperture of the
optics,
, is defined as
radiant power incident per unit area onto a target, in this case
typically the effective aperture of the
optics, 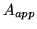 , image area,
, image area, 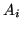 ,
area of CCD-detector,
,
area of CCD-detector, 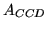 , or the
area of a CCD pixel,
, or the
area of a CCD pixel, 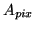 .
.
The transmittance,
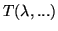 , of an optical
system is a function of many parameters, for example wavelength
, of an optical
system is a function of many parameters, for example wavelength
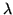 , viewing angle, temperature, etc., and must be
experimentally determined (See Chapter 4). Here it is enough
to state that the total transmittance is given by the product of the
individual transmittances of the various components of the optical
system:
, viewing angle, temperature, etc., and must be
experimentally determined (See Chapter 4). Here it is enough
to state that the total transmittance is given by the product of the
individual transmittances of the various components of the optical
system:
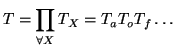 |
(3.9) |
Where 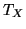 is exemplified by
is exemplified by 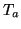 ,
, 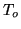 and
and 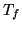 which are the transmittance of the atmosphere,
optics and filter, respectively. In the following text
which are the transmittance of the atmosphere,
optics and filter, respectively. In the following text 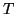 will denote the product of appropriate transmittances according to
Equation 3.9.
will denote the product of appropriate transmittances according to
Equation 3.9.
Consider an extended source of area, 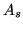 , of
given column emission rate,
, of
given column emission rate, 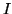 , imaged by an
optical system, here represented by a single lens with given
focal length,
, imaged by an
optical system, here represented by a single lens with given
focal length, 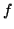 , and
f-number,
, and
f-number, 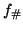 . The relation between the
aperture-stop,
. The relation between the
aperture-stop, 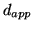 , f and
, f and 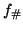 is given by:
is given by:
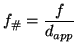 |
(3.10) |
Setting the source at distance 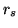 from the lens, which is
at the distance
from the lens, which is
at the distance 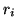 from the detector and letting
from the detector and letting
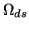 be the solid angle of the lens aperture
as seen from the source, (assuming small angles), the
photon flux,
be the solid angle of the lens aperture
as seen from the source, (assuming small angles), the
photon flux,
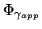 , at the lens
aperture then becomes:
, at the lens
aperture then becomes:
![$\displaystyle \Phi_{\gamma_{app}}=L_{\gamma}A_{s}T_{a}\Omega_{ds}= L_{\gamma}A_...
..._{a}\frac{A_{app}}{r_{s}^{2}}\ \left[\frac{\mathrm{photons}}{\mathrm{s}}\right]$](img141.png) |
(3.11) |
The spectral radiant incidence at the
aperture,
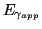 , then
becomes:
, then
becomes:
![$\displaystyle E_{\gamma_{app}}=\frac{\Phi_{\gamma_{app}}}{A_{app}}= \frac{L_{\g...
...A_{s}T_{a}}{r_{s}^{2}}\ \left[\frac{\mathrm{photons}}{\mathrm{s}\ m^{2}}\right]$](img144.png) |
(3.12) |
The spectral radiant incidence at the image
plane,
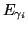 , is
given by (by substituting Equation 3.10 and assuming a circular aperture):
, is
given by (by substituting Equation 3.10 and assuming a circular aperture):
![$\displaystyle E_{\gamma_{i}}=\frac{\Phi_{\gamma_{app}}}{A_{i}}= L_{\gamma}\frac...
...{s}^2f_{\char93 }^{2}}\ \left[\frac{\mathrm{photons}}{\mathrm{s}\ m^{2}}\right]$](img146.png) |
(3.13) |
Noting that, for thin lenses and small angles:
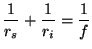 |
(3.14) |
In this case:
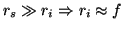 |
(3.15) |
The lens-magnification formula is:
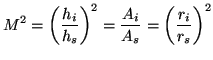 |
(3.16) |
where 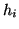 and
and 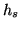 denote the height of the
image and source respectively. Inserting Equations 3.6 and
3.14-3.16 into Equation 3.13, the following
equation for
denote the height of the
image and source respectively. Inserting Equations 3.6 and
3.14-3.16 into Equation 3.13, the following
equation for
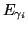 is obtained:
is obtained:
![$\displaystyle E_{\gamma_{i}}=\frac{T\Phi_{\gamma}}{A_{i}}= TL_{\gamma}\frac{\pi...
...0}I}{16f_{\char93 }^{2}}\ \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2}}\right]$](img152.png) |
(3.17) |
Note that this equation is only accurate for small angles, an off-axis
image will have reduced incidence compared to an on-axis image. This
is called the ``natural vignetting'',
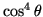 ,
and is usually inserted as a multiplication factor in Equation 3.17, as
required.
,
and is usually inserted as a multiplication factor in Equation 3.17, as
required.
However, the actual vignetting is highly dependent on the
characteristics of the optical system. Therefore the vignetting as well as
other aberrations, and the transmittance ( ) must be
experimentally determined. This will be considered further in
Chapter 4 and references therein.
) must be
experimentally determined. This will be considered further in
Chapter 4 and references therein.
Using Equation 3.17 the number of photons reaching the
image plane,
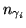 , can be calculated:
, can be calculated:
![$\displaystyle n_{\gamma_{i}}= E_{\gamma_{i}}t_{\mathit{int}}A_{i}= T t_{\mathit{int}}A_{i}\frac{10^{10}I}{16f_{\char93 }^{2}}\ \left[\mathrm{photons}\right]$](img156.png) |
(3.18) |
Here
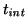 is the integration time in seconds. The
number of photons hitting the
CCD,
is the integration time in seconds. The
number of photons hitting the
CCD,
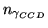 , are:
, are:
![$\displaystyle n_{\gamma_{CCD}}= n_{\gamma_{i}} T_{w} T_{CCD} \frac{A_{CCD}}{A_{i}}\ \left[\mathrm{photons}\right]$](img159.png) |
(3.19) |
Here 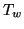 is the transmittance of the optical window
protecting the CCD, and
is the transmittance of the optical window
protecting the CCD, and 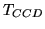 is the transmittance of the
CCD substrate (in the case of a back-side illuminated CCD). Likewise,
the number of photons hitting an individual
pixel,
is the transmittance of the
CCD substrate (in the case of a back-side illuminated CCD). Likewise,
the number of photons hitting an individual
pixel,
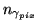 , is:
, is:
![$\displaystyle n_{\gamma_{pix}}= n_{\gamma_{CCD}}\frac{A_{pix}}{A_{CCD}}= T t_{\...
...{int}}A_{pix}\frac{10^{10}I}{16f_{\char93 }^{2}}\ \left[\mathrm{photons}\right]$](img163.png) |
(3.20) |
(using Equations 3.18-3.19 and
Equation 3.20). Again, please remember the caution at the end of
Section 3.1.3
``During the past couple of decades the Charge Coupled
Device (CCD) sensor has gradually replaced the tube type sensors,
such as the vidicon, due to its advantages in size, weight, power
consumption, noise characteristics, linearity, dynamic range,
photometric accuracy, spectral responsitivity, geometric stability,
reliability, and durability'' [Janesick et al., 1987]. As an auroral
imager, the CCD is thus almost an ideal detector for ground-based as
well as for space-borne instruments. The CCD can be used either as the
primary photon detector, or in an Intensified CCD (ICCD)
configuration. Whether to use a CCD or an ICCD is mainly a matter of
requirements on temporal resolution and signal-to-noise
ratio,
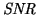 . This section will begin with a short review
of a number of parameters describing the performance of a CCD
detector.
. This section will begin with a short review
of a number of parameters describing the performance of a CCD
detector.
Quantum efficiency
The quantum efficiency, 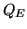 ,
is a measure of the number of electrons generated per incident
photon:
,
is a measure of the number of electrons generated per incident
photon:
![$\displaystyle {Q_{E}}=\eta_{E}Q_{EI} \left[\frac{e^{-}}{\mathrm{photons}}\right]$](img167.png) |
(3.21) |
where 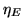 is the effective quantum yield
(electrons generated, collected, and transferred per interacting
photon per pixel) and
is the effective quantum yield
(electrons generated, collected, and transferred per interacting
photon per pixel) and 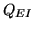 is the interacting quantum
efficiency (interacting photons per incident photons per pixel)
[Janesick et al., 1987]. However, for the purpose of this text it is
only needed to consider
is the interacting quantum
efficiency (interacting photons per incident photons per pixel)
[Janesick et al., 1987]. However, for the purpose of this text it is
only needed to consider 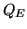 , which for the purpose of this
text, is the same as the detective quantum efficiency (DQE).
, which for the purpose of this
text, is the same as the detective quantum efficiency (DQE).
Quantum efficiency for a CCD is wavelength dependent, and is of no
value unless the wavelength is specified. High performance scientific
thinned, back-side illuminated anti-reflection coated CCD devices
might have as high quantum efficiency as 80-90% in the visible
region as demonstrated in Figure 3.1.
Figure 3.1:
Quantum efficiency vs. wavelength for the SI-003AB CCD (ALIS
ccdcam5) as published in the manufacturers data-sheet.
Four curves are presented: with standard anti-reflection coating
(``StdAR'') UV anti-reflection coating (``UVAR''), uncoated,
thinned, back-side illuminated (``Thinned uncoated'') and
front-side illuminated (``Frontside''). The ALIS imagers have a
standard anti-reflection coating.
|
|
As a comparison, 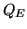 for typical consumer CCDs lies in the range
30-70%.
The average number of photoelectrons,
for typical consumer CCDs lies in the range
30-70%.
The average number of photoelectrons,
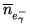 ,
obtained from
,
obtained from
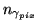 (Equation 3.20) is:
(Equation 3.20) is:
![$\displaystyle \overline{n}_{e^{-}_{\gamma}}={Q_{E}}n_{\gamma_{pix}} \left[e^{-}\right]$](img173.png) |
(3.22) |
Noise
Aurora and airglow are so-called photon-limited signals, where the
quantum nature of light limits the achievable signal-to-noise ratio.
Photon arrival follows Poisson statistics, where the variance is equal
to the mean. The sum of the standard deviation of the noise
resulting from the photoelectrons,
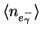 , and dark-current
noise,
, and dark-current
noise,
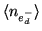 , is denoted shot
noise,
, is denoted shot
noise,
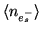 , and is obtained from the
following equation:
, and is obtained from the
following equation:
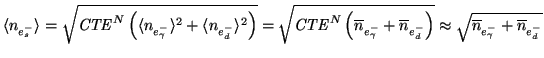 |
(3.23) |
Here
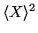 stands for the variance of quantity
stands for the variance of quantity
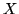 and
and
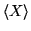 is the standard deviation.
is the standard deviation.
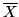 denotes the mean value.
denotes the mean value.
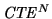 stands for the Charge Transfer Efficiency (
stands for the Charge Transfer Efficiency (
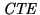 ) where
) where
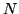 is the number of transfers. Usually
is the number of transfers. Usually
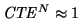 for reasonably sized CCD devices.
Note that
for reasonably sized CCD devices.
Note that
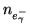 would be present even for an ideal detector.
would be present even for an ideal detector.
Additional noise sources include: reset noise, on-chip and off-chip
amplifier noise (1/f-noise and white noise). Of particular interest
for low-light applications is that the 1/f-noise, which is the main
source of the read noise (``noise-floor''), increases in proportion to
the square root of the read-out frequency (``pixel-clock''), thus
requiring a suitable compromise between noise performance and
frame-rate. The analogue-to-digital converter has a quantisation
noise, also switching transients coupled through the clock signals,
electro-magnetic interference, etc., sums up to the total noise.
There is pattern noise due to differences in dark-current and photo
response non-uniformities [Holst, 1998]. At high signal levels
the total noise is dominated by pattern noise (pixel to pixel
sensitivity variations within the CCD) for most CCDs, at low signal
levels the read noise (``noise floor'') dominates
[Janesick et al., 1987]. Many of these noise sources can be reduced to
negligible levels by good electronic design practices. In particular,
the dark-current (and reset noise) is reduced by cooling the CCD. By
the use of Double Correlated Sampling (DCS) the reset noise
can be almost eliminated. The quantisation noise is eliminated by
using a sufficiently high resolution ADC. It is, however, beyond the
scope of this work to embark onto a detailed analysis of the
noise-sources in CCD imagers, instead a simplified noise model from
Holst [1998] is adopted:
![$\displaystyle \langle n_{e^{-}_{CCD}} \rangle =\sqrt{ \langle {n_{e^{-}_{s}}} \...
...}} \rangle^{2}+\langle {n_{e^{-}_{p}}} \rangle^{2}}\ \left[{e^{-}_{RMS}}\right]$](img187.png) |
(3.24) |
The standard deviation of the noise floor (or read
noise),
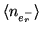 , is usually stated in the imager
specification as `read noise', or easily obtained from a zero
exposure. This noise source increases with the square-root of the
pixel clock frequency, which imposes an
, is usually stated in the imager
specification as `read noise', or easily obtained from a zero
exposure. This noise source increases with the square-root of the
pixel clock frequency, which imposes an
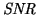 constraint onto
the frame-rate.
constraint onto
the frame-rate.
The pattern noise,
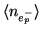 , is the sum of
Fixed Pattern Noise (FPN), resulting from pixel-to-pixel
variations in the dark-current, and Photo Response
Non-Uniformities (PRNU). An approximate worst case value is provided by
Holst [1998]:
, is the sum of
Fixed Pattern Noise (FPN), resulting from pixel-to-pixel
variations in the dark-current, and Photo Response
Non-Uniformities (PRNU). An approximate worst case value is provided by
Holst [1998]:
![$\displaystyle \langle n_{e^{-}_{p}} \rangle =\sqrt{\langle {n_{e^{-}_{FPN}}} \r...
...line{n}_{e^{-}_{\gamma}}}{\sqrt{{n_{e^{-}_{max}}}}}\ \left[{e^{-}_{RMS}}\right]$](img190.png) |
(3.25) |
However, for the low signal levels considered here, pattern noise is
neglected. Then the total noise approximation for a bare CCD becomes
(by substituting Equation 3.23 into Equation 3.24):
![$\displaystyle \langle n_{e^{-}_{CCD}} \rangle \approx \sqrt{\overline{n}_{e^{-}...
...n}_{e^{-}_{d}}+\langle {n_{e^{-}_{r}}} \rangle^{2}}\ \left[{e^{-}_{RMS}}\right]$](img191.png) |
(3.26) |
It should be remembered that this equation is an approximation.
Signal-to-noise ratio
The measured signal-to-noise ratio in terms of the digital
output,
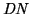 , or in terms of
root-mean-square electrons
, or in terms of
root-mean-square electrons
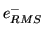 is defined as follows:
is defined as follows:
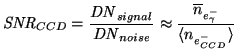 |
(3.27) |
Substituting Equation 3.26 the
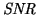 can now be calculated
with the help of Equations 3.20 and 3.22 and the total noise is given by
Equation 3.26:
can now be calculated
with the help of Equations 3.20 and 3.22 and the total noise is given by
Equation 3.26:
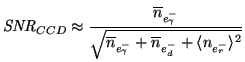 |
(3.28) |
For an ideal photon detector Equation 3.28 becomes:
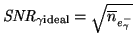 |
(3.29) |
The signal-to-noise ratio of an ICCD
In the image-intensifier, for each primary photoelectron emitted
by the photo-cathode (
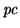 ), the image-intensifier
produces a burst of approximately
), the image-intensifier
produces a burst of approximately 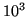 secondary CCD electrons,
typically by the use of a micro-channel plate (MCP) between
the photo-cathode and phosphor screen. The phosphor screen is then
optically coupled to the CCD by the use of lenses or a fibre-optic
taper3.2.
secondary CCD electrons,
typically by the use of a micro-channel plate (MCP) between
the photo-cathode and phosphor screen. The phosphor screen is then
optically coupled to the CCD by the use of lenses or a fibre-optic
taper3.2.
The number of photons reaching the image plane
(
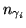 ) is given by Equation 3.18. The average
number of signal electrons generated by the
photo-cathode,
) is given by Equation 3.18. The average
number of signal electrons generated by the
photo-cathode,
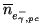 , for a pixel
area
, for a pixel
area 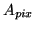 projected onto the photo-cathode, by the
fibre-optic minification ratio,
projected onto the photo-cathode, by the
fibre-optic minification ratio, 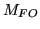 is given
by [see Holst, 1998, p. 196]:
is given
by [see Holst, 1998, p. 196]:
![$\displaystyle \overline{n}_{e^{-}_{\gamma{},pc}}= {Q_{E_{pc}}}\overline{n}_{e^{...
..._{pix} \frac{10^{10}I}{16f_{\char93 }^{2}}\ \left[\mathrm{{e^{-}_{RMS}}}\right]$](img202.png) |
(3.30) |
After the MCP the number of electrons are amplified with the
average MCP gain,
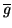 , i.e. average
number of secondary
photoelectrons,
, i.e. average
number of secondary
photoelectrons,
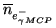 ,
produced per photo-cathode electron
,
produced per photo-cathode electron
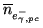
![$\displaystyle \overline{n}_{e^{-}_{\gamma{}MCP}}= \overline{g}\,\overline{n}_{e^{-}_{\gamma,pc}}\ \left[\mathrm{{e^{-}_{RMS}}}\right]$](img206.png) |
(3.31) |
The photoelectrons are then converted back to photons by the phosphor
screen with a phosphor efficiency, 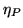 , and then
re-imaged onto the CCD via a fibre optic taper. The transmittance
losses here are denoted
, and then
re-imaged onto the CCD via a fibre optic taper. The transmittance
losses here are denoted 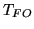 . Finally the photons hit the
CCD and are converted to photoelectrons:
. Finally the photons hit the
CCD and are converted to photoelectrons:
![$\displaystyle \overline{n}_{e^{-}_{\gamma{}CCD}}= \eta_{P}Q_{E_{CCD}}T_{FO}\,\overline{n}_{e^{-}_{\gamma{}MCP}}\ \left[\mathrm{{e^{-}_{RMS}}}\right]$](img209.png) |
(3.32) |
By applying the following approximation:
the
following equation is obtained (using
Equations 3.30-3.32):
![$\displaystyle \overline{n}_{e^{-}_{\gamma CCD}}= \overline{g}\,\overline{n}_{e^...
..._{pix} \frac{10^{10}I}{16f_{\char93 }^{2}}\ \left[\mathrm{{e^{-}_{RMS}}}\right]$](img211.png) |
(3.33) |
As with the CCD (see Equation 3.23), the photo-cathode produces both
photon-noise and dark-current noise:
![$\displaystyle \langle n_{e^{-}_{s,pc}} \rangle =\sqrt{ \langle {n_{e^{-}_{\gamm...
...}+ \langle {n_{e^{-}_{d,pc}}} \rangle^{2}}\ \left[\mathrm{{e^{-}_{RMS}}}\right]$](img212.png) |
(3.34) |
Another noise source, unique to the ICCD, is the electron
multiplication noise, which is due to the statistical distribution
of the number of secondary photoelectrons3.3.
Taking this uncertainty in
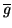 into account, the
combined variance with the photon noise becomes:
into account, the
combined variance with the photon noise becomes:
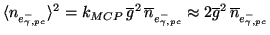 |
(3.35) |
Here, 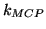 is the microchannel excess noise.
The photo-cathode dark-current noise, is also dependent on
is the microchannel excess noise.
The photo-cathode dark-current noise, is also dependent on
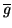 in the same way:
in the same way:
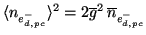 |
(3.36) |
Taking Equation 3.26 as an approximation for the total CCD noise,
and inserting into it Equations 3.35 and 3.36, for the ICCD noise
sources, leads to the following expression for the total
noise for the ICCD,
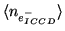 :
:
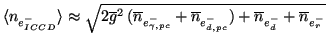 |
(3.37) |
By applying Equations 3.33 and 3.37 into Equation 3.27 the following
approximation for the
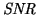 of an ICCD,
of an ICCD,
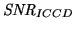 ,
emerges:
,
emerges:
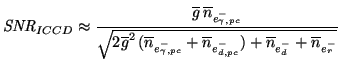 |
(3.38) |
As seen, increasing the gain of the image intensifier makes the CCD
noise-sources negligible, but does not increase the
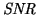 . For very high gain, Equation 3.38 is reduced to:
. For very high gain, Equation 3.38 is reduced to:
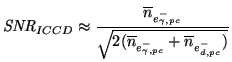 |
(3.39) |
Threshold of detection and maximum signal
The threshold of detection is usually defined as
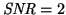 while
the Noise Equivalent Exposure,
while
the Noise Equivalent Exposure,
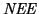 , is obtained when
, is obtained when
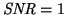 . The maximum signal, or Saturation Equivalent
Exposure (SEE) is obtained when the charge well
capacity,
. The maximum signal, or Saturation Equivalent
Exposure (SEE) is obtained when the charge well
capacity,
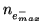 , is reached. This occurs when:
, is reached. This occurs when:
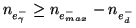 |
(3.40) |
In most cases the maximum charge-well
capacity,
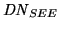 , is matched to the
maximum ADC output
, is matched to the
maximum ADC output
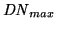 . For the ICCD case, apart
from the condition above, there is also a saturation level for the
image intensifier to be considered. On the other hand, the
high-voltage for the intensifier can be gated, acting like an
electronic shutter.
. For the ICCD case, apart
from the condition above, there is also a saturation level for the
image intensifier to be considered. On the other hand, the
high-voltage for the intensifier can be gated, acting like an
electronic shutter.
The Dynamic Range,
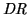 , is defined as the peak
signal divided by the RMS noise and the
DC-bias-level,
, is defined as the peak
signal divided by the RMS noise and the
DC-bias-level,
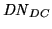 , (if any).
The minimum ADC output,
, (if any).
The minimum ADC output,
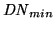 , is subtracted
in the case of a signed integer output.
, is subtracted
in the case of a signed integer output.
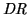 is usually expressed in
decibels.
is usually expressed in
decibels.
![$\displaystyle \mathit{DR}= 20 \log_{10} \left( \frac{\mathit{DN}_{SEE}-\mathit{DN}_{min}} {\mathit{DN}_{DC}+\mathit{DN}_{NEE}-\mathit{DN}_{min}} \right) [dB]$](img233.png) |
(3.41) |
An approximate theoretical value for
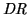 is obtained by dividing the
maximum signal (Equation 3.40) by the total
noise,
is obtained by dividing the
maximum signal (Equation 3.40) by the total
noise,
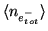 , which is found in
Equations 3.26 and 3.37 for the CCD and ICCD case
respectively.)
, which is found in
Equations 3.26 and 3.37 for the CCD and ICCD case
respectively.)
![$\displaystyle \mathit{DR}\approx 20 \log_{10} \frac{n_{e^{-}_{max}}- n_{e^{-}_{d}}}{\langle n_{e^{-}_{tot}} \rangle }\ [dB]$](img235.png) |
(3.42) |




Next: Selecting an imager for
Up: The ALIS Imager
Previous: The ALIS Imager
Contents
Index
copyright Urban Brändström
![$\displaystyle L_{E}(\lambda)=\frac{\partial^{2}\Phi(\lambda)}{\partial A_{s}\partial\Omega}\ \left[\frac{\mathrm{W}}{\mathrm{m^2\ sr}}\right]$](img92.png)
![$\displaystyle L_{E}(\lambda)=\frac{\partial^{2}\Phi(\lambda)}{\partial A_{s}\partial\Omega}\ \left[\frac{\mathrm{W}}{\mathrm{m^2\ sr}}\right]$](img92.png)
![]() extending away from the detector into the source. The volume emission
rate from a volume element of length
extending away from the detector into the source. The volume emission
rate from a volume element of length ![]() at distance
at distance ![]() is
is
![]() . The contribution to
. The contribution to
![]() is given
by:
is given
by:
![$\displaystyle dL_{\gamma}=\frac{\epsilon(l,t,\lambda)}{4\pi}\,dl\ \left[\frac{\mathrm{photons}}{\mathrm{s\ m^2\ sr}}\right]$](img107.png)
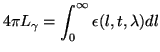
![]() Lux3.1. By the use of Equations 3.2 and 3.6, the
spectral radiant sterance in energy units (
Lux3.1. By the use of Equations 3.2 and 3.6, the
spectral radiant sterance in energy units (![]() ) can be
calculated:
) can be
calculated:
![$\displaystyle L_{E}(1\ \mathrm{[kR]})=\frac{10^{13} hc}{4\pi\lambda}= \frac{10^{3}hc}{4\pi\times5577} \approx 300 \left[\frac{nW}{\mathrm{s\ m^2\ sr}}\right]$](img114.png)
![$\displaystyle L_{E}(1\ \mathrm{[MR]})\approx 300 \left[\frac{\mu W}{\mathrm{s\ m^2\ sr}}\right]$](img116.png)
![]() , of an optical
system is a function of many parameters, for example wavelength
, of an optical
system is a function of many parameters, for example wavelength
![]() , viewing angle, temperature, etc., and must be
experimentally determined (See Chapter 4). Here it is enough
to state that the total transmittance is given by the product of the
individual transmittances of the various components of the optical
system:
, viewing angle, temperature, etc., and must be
experimentally determined (See Chapter 4). Here it is enough
to state that the total transmittance is given by the product of the
individual transmittances of the various components of the optical
system:
![]() , of
given column emission rate,
, of
given column emission rate, ![]() , imaged by an
optical system, here represented by a single lens with given
focal length,
, imaged by an
optical system, here represented by a single lens with given
focal length, ![]() , and
f-number,
, and
f-number, ![]() . The relation between the
aperture-stop,
. The relation between the
aperture-stop, ![]() , f and
, f and ![]() is given by:
is given by:
![]() ) must be
experimentally determined. This will be considered further in
Chapter 4 and references therein.
) must be
experimentally determined. This will be considered further in
Chapter 4 and references therein.
![]() . This section will begin with a short review
of a number of parameters describing the performance of a CCD
detector.
. This section will begin with a short review
of a number of parameters describing the performance of a CCD
detector.
![\includegraphics[width=\textwidth]{eps/imager/qe.eps}](img170.png)
![]() , is the sum of
Fixed Pattern Noise (FPN), resulting from pixel-to-pixel
variations in the dark-current, and Photo Response
Non-Uniformities (PRNU). An approximate worst case value is provided by
Holst [1998]:
, is the sum of
Fixed Pattern Noise (FPN), resulting from pixel-to-pixel
variations in the dark-current, and Photo Response
Non-Uniformities (PRNU). An approximate worst case value is provided by
Holst [1998]:
![]() ), the image-intensifier
produces a burst of approximately
), the image-intensifier
produces a burst of approximately ![]() secondary CCD electrons,
typically by the use of a micro-channel plate (MCP) between
the photo-cathode and phosphor screen. The phosphor screen is then
optically coupled to the CCD by the use of lenses or a fibre-optic
taper3.2.
secondary CCD electrons,
typically by the use of a micro-channel plate (MCP) between
the photo-cathode and phosphor screen. The phosphor screen is then
optically coupled to the CCD by the use of lenses or a fibre-optic
taper3.2.
![]() ) is given by Equation 3.18. The average
number of signal electrons generated by the
photo-cathode,
) is given by Equation 3.18. The average
number of signal electrons generated by the
photo-cathode,
![]() , for a pixel
area
, for a pixel
area ![]() projected onto the photo-cathode, by the
fibre-optic minification ratio,
projected onto the photo-cathode, by the
fibre-optic minification ratio, ![]() is given
by [see Holst, 1998, p. 196]:
is given
by [see Holst, 1998, p. 196]:
![]() :
: