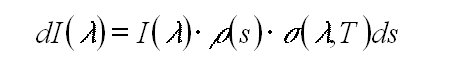T. Wagner¹, C.F. Enell²

¹Institut für Umweltphysik, University of Heidelberg, Germany

²Institutet för Rymdfysik, Kiruna, Sweden
 
 

Introduction

UV-vis absorption spectroscopy using extraterrestrial light sources is a widely used technique for the measurement of atmospheric trace gases, in particular for remote sensing of stratospheric species. BrO and OClO show characteristic absorption features in the UV-vis spectral range which can be detected in spectra of zenith scattered light measured at the ground. The DOAS technique allows to identify and quantify the absorption of these species. In sections 1 to 6 a general description of the DOAS method and its application to ground based measurements of zenith scattered light is given. The specific details of the BrO and OClO analysis are presented in sections 7 and 8.
 
 

1 The Beer-Lambert Law

The absorption of radiation by matter is described by the Beer-Lambert law. The absorption of light of the intensity I(l ) at the wavelength l as it passes through an infinitesimally thin layer of an absorbing matter ds is:
 
 

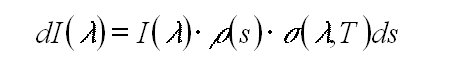    (1)
 
 

Here s(l ,T) is the absorption cross section of the absorbing species which depends on the wavelength and temperature and r(s) is its concentration. Integration of equation 1 for a finite light path through the absorbing species leads to the relationship between the incident light intensity I₀(l ) and the transmitted light intensity I(l ), known as the Beer-Lambert law:
 
 

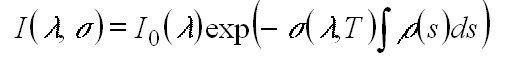    (2)
 
 

The logarithm of the ratio of the measured I and I₀ is called optical density t(l ).

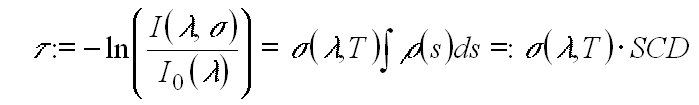    (3)

From t(l ) the (slant) column density SCD :=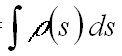of the absorbing species can be calculated; if the concentration is constant along the absorption path the concentration can be derived.
 
 

2 Differential optical absorption spectroscopy (DOAS)

The Beer-Lambert law can not directly be applied to atmospheric measurements because of several reasons:

a) Besides the absorption of the trace gases light extinction occurs also due to scattering on molecules and aerosols. Especially for aerosols this extinction can not be corrected for with the desired accuracy.

b) In the atmosphere the absorptions of several species always add up to the total absorption. Thus in most of the cases it is not possible to measure one specific species.

c) In the case of satellite measurements the detected intensity can strongly depend on the ground albedo.

These restrictions can be avoided by applying the method of differential optical absorption spectroscopy (DOAS).

The DOAS technique relies on the measurement of absorption spectra instead of the intensity of monochromatic light (Equation 2). Thus it is possible to separate the absorption structures of several atmospheric species from each other as well as from the extinction due to scattering on molecules and aerosols. The DOAS method was introduced by Perner and Platt [1979], and a detailed description can be found in Platt [1994].

The key principle of DOAS is the separation of the absorption in a part which represents broad spectral features and in a part representing narrow spectral features. Consequently s(l ) of a certain absorbing species is split into a portion s_c(l ) which varies only 'slowly' with the wavelength land into a portion s ' (l ) which shows 'rapid' variation with l:

s(l ) = s_c(l ) + s '(l ).   (4)

The definition of the threshold between 'slow' and 'rapid' variation of the absorption cross-section as a function of wavelength depends on the observed wavelength interval and the width of the absorption bands to be detected. Commonly the spectra are filtered by dividing by a fitted polynomial or by a smoothed spectrum. Conventionally s ' (l ) is called differential absorption cross-section (see Figure 1).
 

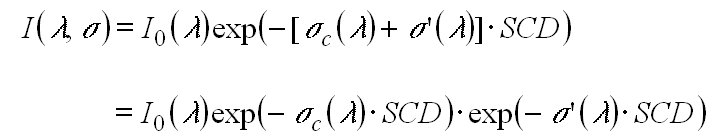     (5)
 

Accordingly the differential optical density t ' (l ,s ,s') can be determined, which is defined as
 

t ' (l ,s ,s') := ln [I(l ,s -s')/I(l ,s )].     (6)
 

In practice I(l ,s -s ') is determined applying the similar high pass filter to the measured spectrum.

Combining Equation 3 and Equation. 6, it follows immediately that
 

t ' (l ,s ,s') = t(l ,s ) - t (l ,s -s').   (7)
 

This is demonstrated also on Figure 1. The slant column density of a desired trace species can now be calculated
 

SCD' := t' (l ,s ,s') / s'.   (8)
 

The new expression SCD' (compared to SCD derived from Equation. 3) indicates that it is calculated from 'differential' quantities.

In the practical DOAS evaluation process the laboratory spectra of different absorbing trace gases are least squares fitted to the atmospheric spectrum. >From the result of the fitting procedure the slant column density can be determined. Because several absorbing trace gases

can be simultaneously detected by their specific spectral absorption features the DOAS method is widely used for atmospheric measurements.

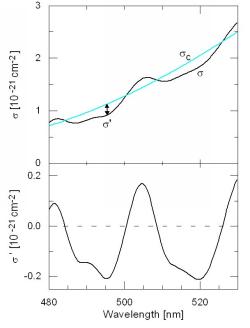
Figure 1 Splitting of the absorption cross section into a 'slowly' and 'rapidly' varying part [adapted from Otten, pers. communication].
 
 

3 The spectral fitting process

The measured spectrum is fitted by the absorption spectra of the trace gases absorbing in the respective spectral range and a polynomial of a specified degree by means of a non linear least squares fitting algorithm [Gomer et al., 1993; Stutz and Platt, 1996]. This fitting algorithm uses the Levenberg-Marquard method [Levenberg, 1944; Marquardt, 1963] which is an iterative combination of a linear part for the retrieval of the trace gas absorptions and a non linear part which accounts for possible spectral shifts between the measured spectrum and the reference spectrum.

Since the spectra are recorded with a diode array of 1024 discrete elements the obtained signal by a single diode represents the integrated intensity over the wavelength range which is covered by this diode:
 

I(l_i) =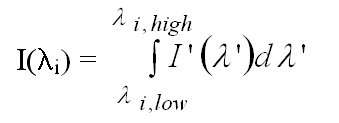     (9)
 

Here l_i denotes the centre wavelength of the diode element, l_i,low the shortest wavelength and l_i,high the longest wavelength covered by the element.

The aim of the linear fitting process is to minimise the sum over the measured optical depths t '(l_i) of the individual diode elements of the selected wavelength range:
 
 

½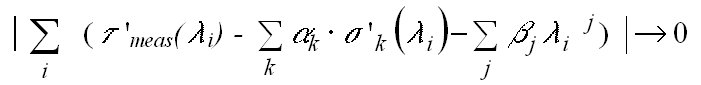(t '_meas(l_i) -         (10)
 

Here s_k'(l_i) denotes the differential cross section of the k-th trace gas taken into account by the fitting routine. The derived fit coefficient a_k is the desired SCD of this species. 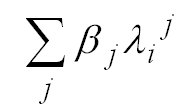is a polynomial often used to account for broad band features, e.g. from Rayleigh- and Mie-scattering. In the second part of the fitting process the wavelength calibration of reference spectra is varied with respect to the measured spectrum to achieve the best match of the absorption features in the measured spectrum. For that purpose the reference spectra are interpolated and the grid points l_i are replaced by the values of the new wavelength l_f(i). For the OClO and BrO evaluations described below linear shifts and also squeezes of the reference spectra were allowed according to f(i) = a + b × i.

For measurements of scattered solar radiation two further spectra are included in the fitting process: one spectrum to correct the Ring-effect (see below) and another to account for the solar Fraunhofer lines which are the most dominant features in the recorded spectra. To remove this structures it is a commonly used method to divide the measured spectra (usually taken at large SZA and thus large atmospheric absorptions) by a spectrum measured at small SZA (and thus small atmospheric absorptions). This spectrum is usually referred to as Fraunhofer reference spectrum. The result of the fitting process then yields the difference of the atmospheric absorptions; thus the absorption of the Fraunhofer spectrum has to be added to derive the total absorption of the measurement. In practice, usually the logarithm of the Fraunhofer spectrum is simultaneously included in the fitting process.

The spectral resolution of DOAS instruments in the UV/vis region is usually in the range of about a few tenths to several nanometers. Thus the natural line widths of the atmospheric absorptions are not resolved. To account for this the absorption cross sections of the trace gases have to be convoluted by the instrumental slit function f(l ) before they are used as input for the fitting routine (equation 10).
 

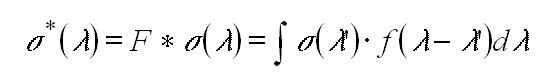     (11)
 

4 The 'solar I₀-effect'

Because of the large number of Fraunhofer lines the intensity of the solar spectrum varies strongly with wavelength. In particular for absorptions showing also narrow spectral structures the absorptions found in measured atmospheric spectra can not be fitted properly by the respective cross sections (which are usually measured in the laboratory using a light source with a smooth spectrum, e.g. a black body radiator). Because these errors arise from the spectral structures of the I₀ spectrum it is usually referred to as solar I₀ effect [Paul Johnston, pers. comm.; Platt et al., 1997, Friess, 1997; Richter, 1997; Van Roozendael et al., 1999b; Wagner, 1999]. While for most of the atmospheric absorbers this leads only to negligible effects in some cases the I₀ effect has to be considered. This is in particular the case when strong atmospheric absorbers like O₃ have to be 'removed' to measure the underlying weak absorptions of other trace gases like BrO. The solar I₀ effect can be accounted for using so called 'I₀ corrected' cross sections. These can be calculated in the following manner: First the highly resolved solar spectrum I₀(l ) is convoluted with the instrument slit function:
 

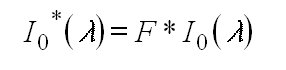     (12)
 

In the next step the absorption spectrum of the chosen trace gas (calculated with a highly resolved cross section and solar spectrum) is convoluted with the instrument slit function:
 

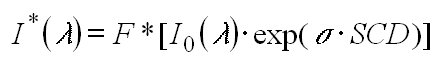     (13)
 

The I₀ corrected cross section is then derived:
 

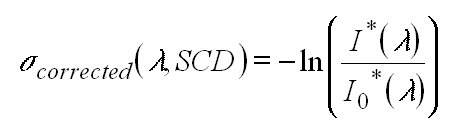     (14)
 

Clearly I₀-corrected cross sections derived in this manner can perfectly match the absorptions in the measured atmospheric spectrum only if the same SCD was used for the calculation which appeared in the atmosphere. However, it turned out that this was not a critical point and the I₀ corrected cross sections could be used for a large range of atmospheric SCDs.
 

5 Correction of the Ring effect

In addition to Rayleigh- and Mie-scattering which are elastic scattering processes in the Earth's atmosphere the solar radiation is also scattered by Raman-scattering whereby the photon's energy changes (see Figure 2). Rotational Raman scattering is thought to be the (most probable) cause for the so called 'Filling in' of the Fraunhofer lines [Bussemer, 1993; Vountas et al., 1998] (and to a lesser degree also of the atmospheric absorption lines [Fish and Jones, 1995]); it was first discovered by Grainger and Ring [1962] and referred to as Ring-effect. Although the Ring effect is only of the order of a few per cent it significantly affects DOAS measurements of scattered radiation: The Fraunhofer lines of the measured spectra can thus not perfectly corrected for by the inclusion of the Fraunhofer spectrum in the fitting process. In consequence structures (up to several per cent in the UV spectral range) remain which mask the weak atmospheric absorptions if the Ring effect is not properly corrected for.
 

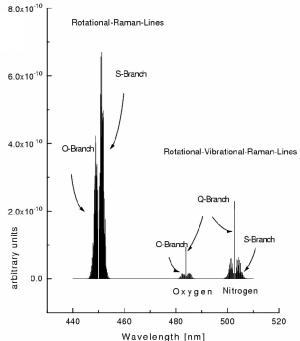
Figure 2 Transitions for rotational and vibrational Raman scattering on O₂ and N₂ molecules (adapted from Haug [1996]).
 

Usually the Ring effect is corrected for by including a further spectrum into the fitting process [Solomon et al., 1987].

The light I_meas detected by the instrument was either scattered in the atmosphere by molecules or aerosols or reflected at the earth's surface. While Rayleigh- and Mie-scattering as well as the reflection are elastic processes, the Raman scattering on molecules introduces an inelastic contribution to the measured light.
 

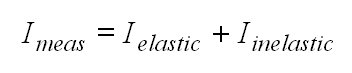     (15)
 

To analyse a measured spectrum the negative logarithm of I_meas is taken (DOAS fitting process, see section 3).

Since I_inelastic is very small (about a few per cent) compared to I_elastic the logarithm can be approximated by the first two terms of the Taylor expansion:
 

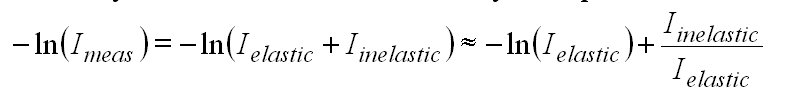     (16)
 

with
 

I_Ring := I_inelastic/I_elastic     (17)
 

I_Ring is usually referred to as Ring spectrum and it can be included in the fitting routine to correct the Ring effect.

From the known energies of the rotational states of the two main gases of the atmosphere, O₂ and N₂, the cross section for rotational Raman scattering can be calculated. This can be done by including Raman scattering into radiative transfer models [Bussemer, 1993; Fish et al., 1995] or by calculating the pure ratio of the cross sections for Raman and Rayleigh scattering.
 

6 Modelling of the atmospheric radiative transport

For the analysis of DOAS measurements using direct or scattered solar radiation traversing the atmosphere, the so-called air mass factor concept has been developed (see e.g. Noxon et al. [1979], Solomon et al. [1987b]). Since the measured slant column density (SCD), the integrated trace gas concentration along the light path, strongly depends on the solar zenith angle (SZA), it is advantageous to convert the SCD into a vertical column density (VCD), the vertically integrated trace gas concentration. This conversion is usually performed by dividing the SCD by the air-mass factor (AMF):
 

VCD = SCD(SZA) / AMF(SZA) (18)
 

Here we use the 'traditional' AMF-approach: First the SCDs of the trace gases are derived from the spectral analysis of the measured spectra. Second these SCDs are converted to VCDs by dividing by the AMF. While this proceeding is convenient and lucid in use, appropriate for many applications and has been widely and successfully used by many groups so far, it should be noted that this separation is not strictly correct [Marquard et al., 2000]. Since BrO and OClO, both species considered here, are only week atmospheric absorbers, the errors caused by the application of the 'traditional' concept are negligible compared to further uncertainties caused by the lack of atmospheric data. In Figure 3 the geometric approximation for the AMF as well as modelled AMFs are displayed.

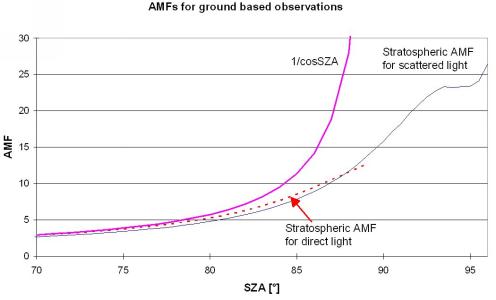
Figure 3 Geometric approximation for the AMF (1/cos[SZA]) compared to stratospheric AMFs for direct and scattered light for zenith scattered light observations (The maximum concentration of the assumed trace gas concentration profile is located at 16 km).
 

While for BrO often the atmospheric VCD is calculated, OClO data are usually presented as SCDs for a SZA of 90 or 92 degrees. For specific applications (e.g. the comparison with model data) BrO and OClO results are presented as so called differential slant column densities (DSCD) which is the difference of the SCD for measurements made at the same day at different SZAs (Usually at 80 and 90 degree SZA).
 

7 Specific properties of the DOAS BrO algorithm

The BrO molecule shows a pronounced spectral structure at wavelengths below 365 nm. For the measurement of scattered light it is difficult to use the spectral regions below 340 nm because the ozone absorptions are getting large which affects several approximations only valid for small absorptions. In particular, also the AMF for BrO shows spectral features [Marquard et al., 2000] which influence the fitting procedure. It turned out that for the BrO analysis of zenith sky measurements the wavelength range between 345 and 359 nm is best suited. This wavelength range is used for the BrO algorithm described in this section. For some cases, in which the measured spectrum and the Fraunhofer reference spectrum are measured within a short period of time (about one week) also a broader spectral range can be applied (345 - 363 nm). This is in particular the case for the determination of daily differential SCDs (DSCDs).
 

7.1 Cross sections

In Table 1 an overview of the reference spectra selected for the BrO algorithm is given. In the selected wavelength range O₃ and NO₂ are the most dominant absorbers. Thus an Io-correction is applied to the respective cross sections (see section 4). The O₄ absorption at 360 shows no spectral fine structure, thus no Io correction was applied. The Ring-spectrum was calculated from the Fraunhofer spectrum according to the approach described in section 5).

For the determination of time series of total columns (SCD or VCD) the measured spectra for long periods (about one year) are evaluated using a single Fraunhofer spectrum. The DSCD evaluation is performed with using daily Fraunhofer reference spectra (SZA = 80°).
 

Reference spectrum	temperature	SCD applied for Io correction	Source
O3	223 K	(1020molec/cm²)	FTS [Voigt et al., 1999a]
O3	246 K	(1020molec/cm²)	FTS [Voigt et al., 1999a]
NO2	223 K	(1017molec/cm²)	FTS [Voigt et al., 1999b]
OClO	204 K	no correction	Wahner et al. [1987]
BrO	228 K	no correction	FTS Wilmouth et al. [1999]
O4	296 K	no correction	Greenblatt et al. [1991]
Ring spectrum	250 K		MFC, Bussemer [1993]
Fraunhofer spectrum	-		for DSCDs:  daily spectra at 80° SZA for SCDs/VCDs:  several selected measured spectra

Table 1 Reference spectra used for the BrO analysis.
 

7.2 Wavelength calibration

The spectral calibration is based on the alignment of the Fraunhofer structures of the measured spectra with those of wavelength calibrated solar intensities from the literature [Kurucz et al., 1984]. This alignment was performed with the software 'WINDOAS' which was developed at the Belgian Institute for Space Aeronomy (BIRA) [M. Van Roozendael, C. Fayt, personal communication]. The high resolved solar spectrum is convoluted and shift and squeeze are allowed. Also included in the fitting process are the reference spectra for O₃ (246 K) and NO₂ (223K), see Table 1. The literature spectra are fitted to a measured spectrum from April 10, 1997, which is also used as Fraunhofer reference spectrum in the DOAS retrieval.

As a result of this fitting procedure the dispersion and the spectral resolution of the instrument is determined (see Figures 4 and 5).
 

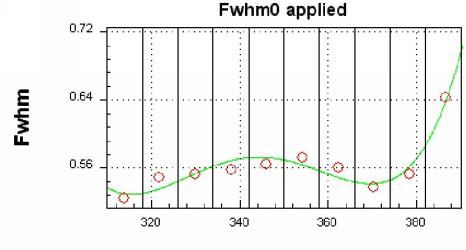Figure 4. Spectral resolution (FWHM) of the measured spectrum from April 10, 1997. This Fit was performed with the software 'WINDOAS' which was developed at the Belgian Institute for Space Aeronomy (BIRA) [M. Van Roozendael, C. Fayt, personal communication].

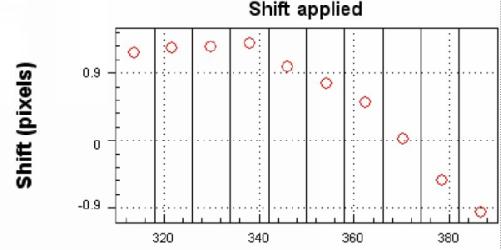Figure 5. Spectral shift (FWHM) of the measured spectrum from April 10, 1997 compared to the spectral calibration performed by measured atomic emission lines. This Fit was performed with the software 'WINDOAS' which was developed at the Belgian Institute for Space Aeronomy (BIRA) [M. Van Roozendael, C. Fayt, personal communication].

The cross sections from the literature (see Table 1) are convoluted using a measured atomic emission line (HG line at 334.15 nm). Since the spectral resolution of the original BrO spectrum (FWHM: 0.4 nm) [Wilmouth et al., 1999] is nearly like that of our own instrument (FWHM: 0.56 nm) it was convoluted with a Gaussian function with a FWHM of only 0.4 nm instead with the measured emission line.

For some applications some additional Fraunhofer have to be used in the spectral BrO retrieval. This is in particular the case when daily DSCDs are determined. In these cases the Fraunhofer spectra are shifted in a fitting procedure to match the spectral calibration of the Fraunhofer spectrum from April 10, 1997. For the determination of the appropriate shift also the O₃ and NO₂ cross sections are included. After this shift the same set of references spectra (as convoluted for April 10, 1997) is applied.
 

7.3 Fitting results and uncertainties

After the raw spectra are subtracted for dark current and offset signals they are divided by the spectrum of a halogen lamp to correct the Fabry-Perrot-Etalon effect and the pixel sensitivity of the Diode array. Offset-, dark current- and lamp spectra are recorded every night automatically.

After taking the logarithm the reference spectra (see Table 1) are fitted to the measured spectrum (also a polynomial of degree 3 is included). The spectra are not smoothed. Shift and squeeze of the spectra is allowed, the shift and squeeze parameters of the different reference spectra are linked. More details can also be found at Wagner, [1994], Otten [1997], Otten et al. [1998], Friess [1999].

In Figure 6 the results of a BrO evaluation are presented.

The statistical error is determined by the fitting routine [Stutz and Platt, 1996]. Typical values are below 10%, see Figure 6. Additional error sources include uncertainties of the wavelength calibration. However, because of the high quality of the wavelength calibration of the novel set of cross sections [Voigt et al., 1999a,b; Wilmouth et al., 1999] these errors are rather small. Possible errors of the absolute values of the BrO cross section can cause systematic errors of the retrieved BrO data.
 

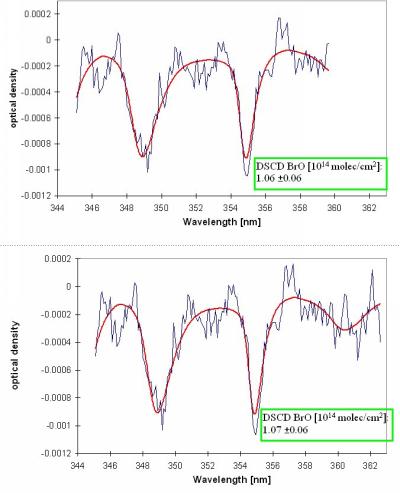
Figure 6 Examples for the BrO evaluation of zenith sky measurement (February 17,1997,7:57, SZA: 85.4°). The thick lines indicate the BrO absorption spectra scaled to the respective absorptions retrieved from the measured spectrum (thin lines).The upper figure shows the standard wavelength range (345-359 nm), the lower figure an extended range (see also text).
 

8 Specific properties of the DOAS OClO algorithm

The OClO molecule shows a pronounced spectral structure at wavelengths below about 420 nm. It turned out that for the OClO analysis of our zenith sky measurements the wavelength range between 363 and 391 nm is best suited.
 

8.1 Cross sections

In Table 2 an overview of the reference spectra selected for the BrO algorithm is given. An Io-correction is applied to the O₃ and NO₂ cross sections (see section 4). The O₄ absorption at 380 shows no spectral fine structure, thus no Io correction was applied. The Ring-spectrum was calculated from the Fraunhofer spectrum according to the approach described in section 5).

For the determination of time series of total columns (SCD or VCD) the measured spectra for long periods (about weeks to months) are evaluated using a single Fraunhofer spectrum. The DSCD evaluation is performed with using daily Fraunhofer reference spectra (SZA = 80°).
 

Reference spectrum	temperature	SCD applied for Io correction	Source
O3	223 K	(1020molec/cm²)	FTS [Voigt et al., 1999a]
NO2	223 K	(1017molec/cm²)	FTS [Voigt et al., 1999b]
OClO	204 K	no correction	Wahner et al. [1987]
O4	296 K	no correction	Greenblatt et al. [1991]
Ring spectrum	250 K		MFC, Bussemer [1993]
Fraunhofer spectrum	-		for DSCDs:  daily spectra at 80° SZA for SCDs/VCDs:  several selected measured spectra

Table 2 Reference spectra used for the OClO analysis.
 

8.2 Wavelength calibration

The wavelength calibration was done as described for the BrO evaluation in section 7.2.
 

8.3 Fitting results and uncertainties

The details of the OClO data processing are very similar to those of the BrO evaluation and are described in detail in section 7.3.

In Figure 7 the results of an OClO evaluation is presented.

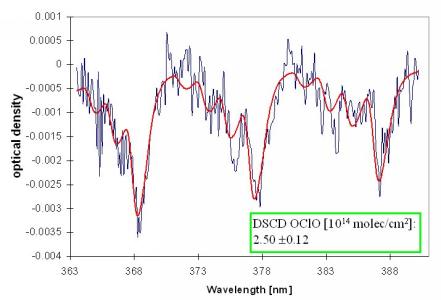
Figure 7 Examples for the OClO evaluation of zenith sky measurement (February 24,1997,15:25, SZA: 90.7°). The thick lines indicate the BrO absorption spectra scaled to the respective absorptions retrieved from the measured spectrum (thin lines).

The statistical error is determined by the fitting routine [Stutz and Platt, 1996]. Typical values are below 10%, see Figure 7. Additional error sources include uncertainties of the wavelength calibration. However, because of the high quality of the wavelength calibration of the novel set of cross sections [Voigt et al., 1999a,b] these errors are rather small. Possible errors of the absolute values of the OClO cross section can cause systematic errors of the retrieved OClO data.
 
 

9 References